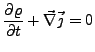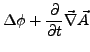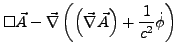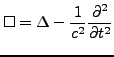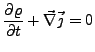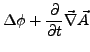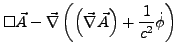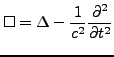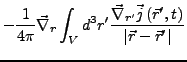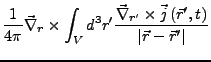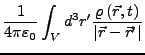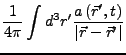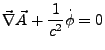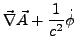Vollständige Maxwell Gleichungen

Vollständige

Maxwell Gleichungen

$$\vec{\nabla}\vec{D} = \varrho$$

$$\vec{\nabla}\times\vec{E}+\dot{\vec{D}} =$$ 0

$$\vec{\nabla}\vec{B} =$$ 0

$$\vec{\nabla}\times\vec{H} = \vec{j}+\dot{\vec{D}}$$

Kontinuitätsgleichung

$$\frac{\partial\varrho}{\partial t}+\vec{\nabla}\vec{j}=0$$

Felder in Medien

empirische Näherung

$$\vec{D} = \underline{\varepsilon_{r}}\varepsilon_{0}\vec{E}$$

$$\vec{B} = \underline{\mu_{r}}\mu_{0}\vec{H}$$

$$\vec{j} = \underline{\sigma}\vec{E}$$

Potentiale

diese lösen die beiden homogenen Maxwellgleichungen automatisch

$$\vec{B} = \vec{\nabla}\times\vec{A}$$

$$\vec{E} = -\vec{\nabla}\phi-\dot{\vec{A}}$$

Potential-DGL's

sind umgeformte inhomogene Maxwell Gleichungen

$$\Delta\phi+\frac{\partial}{\partial t}\vec{\nabla}\vec{A} = -\frac{\varrho_{0}}{\varepsilon_{0}}$$

$$\square\vec{A}-\vec{\nabla}\left(\left(\vec{\nabla}\vec{A}\right)+\frac{1}{c^{2}}\dot{\phi}\right) = -\mu_{0}\vec{j}$$

D'Alembert-Operator

ist definiert als

$$\square=\Delta-\frac{1}{c^{2}}\frac{\partial^{2}}{\partial t^{2}}$$

Eichfreiheit

bietet die Möglichkeit die Potentiale zu verändern, ohne das sich die Felder ändern (Eichtransformation): 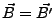$\vec{B}=\vec{B'}$ und $\vec{E}=\vec{E}'$

$$\vec{A}' = \vec{A}+\vec{\nabla}\chi$$

$$\phi' = \phi-\dot{\chi}$$

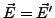
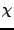• $\chi$ ist beliebieges skalares Feld
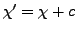• $\chi'=\chi+c$ ist äquivalent

Helmholzt Satz

die Stromdichte 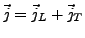$\vec{j}=\vec{j}_{L}+\vec{j}_{T}$ lässt sich in einen longitudinalen und einen tranversalen Anteil aufspalten

$$\vec{j}_{L} = -\frac{1}{4\pi}\vec{\nabla}_{r}\int_{V}d^{3}r'\frac{\vec{\nabla}_{r'}\vec{j}\left(\vec{r}',t\right)}{\left\vert\vec{r}-\vec{r}'\right\vert}$$

$$\vec{j}_{T} = \frac{1}{4\pi}\vec{\nabla}_{r}\times\int_{V}d^{3}r'\frac{\vec{\na... ...r'}\times\vec{j}\left(\vec{r}',t\right)}{\left\vert\vec{r}-\vec{r}'\right\vert}$$

Coulomb-Eichung

bzw. transversal Eichung: wähle 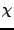$\chi$ so, das

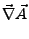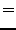$$\vec{\nabla}\vec{A} =$$ 0

dadurch gilt direkt

$$\Delta\phi = -\frac{\varrho_{0}}{\varepsilon_{0}}$$

$$\phi = \frac{1}{4\pi\varepsilon_{0}}\int_{V}d^{3}r'\frac{\varrho\left(\vec{r},t\right)}{\left\vert\vec{r}-\vec{r}'\right\vert}$$

es bleibt nur noch zu lösen

$$\square\vec{A}=-\mu_{0}\vec{j}_{T}$$

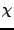• $\chi$ ist nicht Lorenzinvariant!
• Wahl von $\chi$
  

  $$a\left(\vec{r},t\right) = \vec{\nabla}\vec{A}$$

  $$\Delta\chi = -a\left(\vec{r},t\right)$$

  $$\chi = \frac{1}{4\pi}\int d^{3}r'\frac{a\left(\vec{r}',t\right)}{\left\vert\vec{r}-\vec{r}'\right\vert}$$

  
  

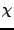
Lorentzeichung

wähle 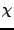$\chi$ so, das

$$\vec{\nabla}\vec{A}+\frac{1}{c^{2}}\dot{\phi}=0$$

dadurch gilt direkt

$$\square\vec{A} = -\mu_{0}\vec{j}$$

$$\square\phi = -\frac{\varrho}{\varepsilon_{0}}$$

• Wahl von $\chi$
  

  $$a\left(\vec{r},t\right) = \vec{\nabla}\vec{A}+\frac{1}{c^{2}}\dot{\phi}$$

  $$\square\chi = -a\left(\vec{r},t\right)$$

  
  

• vollständige Entkopplung von $\vec{A}$ und $\phi$
• $\chi$ ist lorenztinvariant / in jedem Inertialsystem gleich.
• $\chi$ ist nicht eindeutig bestimmt:
  

  $$\square\Lambda\left(\vec{r},t\right) =$$ 0

  $$\chi' = \chi+\Lambda$$