Kovariante Formulierung der Elektrodynamik

Inertialsysteme

Bezugssysteme mit konstanter Relativgeschwindikeit

Ortsvektor

kovariant

$$x^{\mu}=\left(ct,x,y,z\right)$$

Norm

von Kovarianten Vektoren 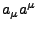$a_{\mu}a^{\mu}$ ist erhalten bei Lorentztransformation

Summenkonvention

für 4-er Vektoren ist, das immer über ein Paar von von Indizes summiert wird, wobei einer unten, und einer oben stehen muss. Beide Vektoren müssen dazu multipliziert geschrieben sein. Summiert wird von 0 bis $3$.

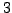Metrischer Tensor

bzw. der Indexverschiebungsoperator ist

$$g_{\mu\nu}=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array}\right)$$

• $g^{\mu\nu}=g_{\mu\nu}$
• $g_{\nu\mu}=g_{\mu\nu}$
• $g_{\mu\nu}x^{\nu}=x_{\mu}$
• $g^{\mu\nu}x_{\nu}=x^{\mu}$

Einheitsmatrix

für 4-er Vektoren

$$\delta_{\mu}^{\nu} = g_{\mu\alpha}g^{\alpha\nu}$$

$$= \left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right)$$

Vierergeschwindigkeit

$u^{\mu}=\frac{dx^{\mu}}{d\tau}$

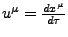
Eigenzeit

$\tau$

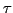
Minkowski-Kraft

$K^{\mu}=m\frac{du^{\mu}}{d\tau}=m\frac{d^{2}x^{\mu}}{d\tau^{2}}=\gamma\left(\frac{\vec{F}\vec{v}}{c},F_{x},F_{y},F_{z}\right)$

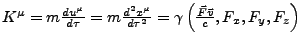
Lorenz-Gamma-Faktor

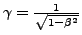$\gamma=\frac{1}{\sqrt{1-\beta^{2}}}$ mit $\beta=\frac{v}{c}$

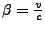
Lorentztransformation

mit der Matrize (hier exemplarisch in 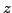$z$ Richtung mit 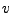$v$ bewegt)

$$L_{\alpha\beta}=\left(\begin{array}{cccc} \gamma & 0 & 0 & -\beta... ...& 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ -\beta\gamma & 0 & 0 & \gamma\end{array}\right)$$

Viererableitung

$\partial_{\mu}=\frac{\partial}{\partial x^{\mu}}=\left(\frac{1}{c}\frac{\parti... ...ial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)$

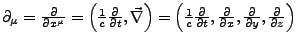
Stromdichte

$j^{\mu}=\left(c\varrho,j_{x},j_{y},j_{z}\right)=\gamma\varrho_{0}\left(c,\vec{v}\right)=\varrho_{0}u^{\mu}$

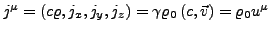
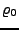• $\varrho_{0}$ ist die Ladungsdichte
• $\vec{j}=\vec{v}\varrho_{0}$

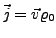
Kontinuitätsgleichung

$\partial_{\mu}j^{\mu}=0$

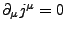
Wellengleichung

$\left(\partial^{\mu}\partial_{\mu}\right)A^{\mu}=\mu_{0}j^{\mu}$

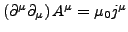
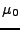• $\mu_{0}$ Permiabilitätskonstante
• $\partial^{\mu}\partial_{\mu}=\square$
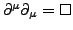
• Gilt nur in Lorentzeichung

Lorentzeichung

$\partial_{\mu}A^{\mu}=0$

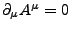
Feldstärketensor

$F^{\mu\nu}=\partial^{\mu}A^{\nu}-\partial^{\nu}A^{\mu}$

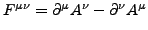
• Antisymmetrisch
  $F^{\mu\nu}=-F^{\nu\mu}$
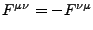
• Komponenten
  $$F^{\mu\nu}=\left(\begin{array}{cccc} 0 & -\frac{1}{c}E_{x} & -\fr... ...& B_{z} & 0 & -B_{x}\\ \frac{1}{c}E_{z} & -B_{y} & B_{x} & 0\end{array}\right)$$

• $F_{\mu\nu}F^{\mu n}=2\left(\vec{B}^{2}-\frac{1}{c^{2}}\vec{E}^{2}\right)$
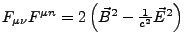
  ist eine Lorentzinvariante

imhomogene Maxwellgleichung

$\partial_{\alpha}F^{\alpha\beta}=\mu_{0}j^{\beta}$

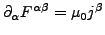
Jakobi-Identität

$\partial^{\alpha}F^{\beta\gamma}+\partial^{\beta}F^{\gamma\alpha}+\partial^{\gamma}F^{\alpha\beta}=0$

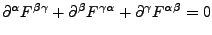
4-dim Epsilontensor

$\varepsilon^{\mu\nu\varrho\sigma}=\begin{cases} +1 & \mbox{gerade Permutation ... ...mutation von }\left(0,1,2,3\right)\\ 0 & \mbox{zwei Indizes gleich}\end{cases}$

Dualrer Feldstärketensor

$\overline{F}^{\mu\nu}=\frac{1}{2}\varepsilon^{\mu\nu\varrho\sigma}F_{\varrho\sigma}$

• $\overline{F}^{\mu\nu}=-\overline{F}^{\nu\mu}$
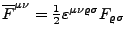
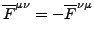
• Komponenten
  $$\overline{F}^{\mu\nu}=\left(\begin{array}{cccc} 0 & -B_{x} & -B_{... ...}{c}E_{x}\\ B_{z} & \frac{1}{c}E_{y} & -\frac{1}{c}E_{x} & 0\end{array}\right)$$

homogene Maxwellgleichung

$\partial_{\alpha}\overline{F}^{\alpha\beta}=0$

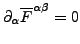
Transformation der Felder

erst für den Spezialfall $\vec{v}=v\vec{e}_{z}$

$$E_{x}' = \gamma\left(E_{x}-\beta cB_{y}\right)$$

$$E_{y}' = \gamma\left(E_{y}+\beta cB_{x}\right)$$

$$E_{z}' = E_{z}$$

$$B_{x}' = \gamma\left(B_{x}+\frac{\beta}{c}E_{y}\right)$$

$$B_{y}' = \gamma\left(B_{y}+\frac{\beta}{c}E_{x}\right)$$

$$B_{z}' = B_{z}$$

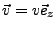
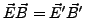• $\vec{E}\vec{B}=\vec{E}'\vec{B}'$ ist Lorentzinvariante
• allgemeiner Fall mit 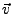$\vec{v}$ in beliebiger Richtung
  

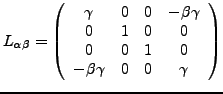
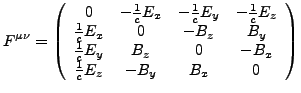
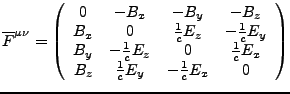
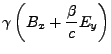
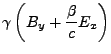
  $$\vec{E}' = \gamma\left[\vec{E}+c\left(\vec{\beta}\times\vec{B}\right)\right]-\frac{\gamma^{2}}{\gamma+1}\vec{\beta}\left(\vec{\beta}\vec{E}\right)$$

  $$\vec{B}' = \gamma\left[\vec{B}-\frac{1}{c}\left(\vec{\beta}\times\vec{E}\right)\right]-\frac{\gamma^{2}}{\gamma+1}\vec{\beta}\left(\vec{\beta}\vec{B}\right)$$