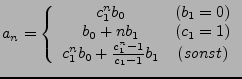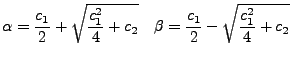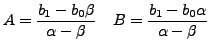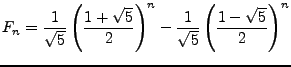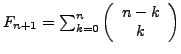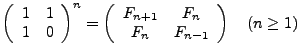Next: Erzeugende Funktionen
Up: Rekursionen
Previous: Rekursionen
Contents
Index
Subsections
Lineare Rekursionsgleichungen
Eine Gleichung der Form
mit den Anfangsbedingungen
heißt lineare Rekursionsgleichung (RG) 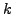 -ter Ordnung.
Für
-ter Ordnung.
Für 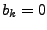 heißt die Gleichung homogen, sonst
inhomogen. Ziel ist es einen geschlossenen Ausdruck
zu finden.
heißt die Gleichung homogen, sonst
inhomogen. Ziel ist es einen geschlossenen Ausdruck
zu finden.
Eine (inhomogene) lineare RG 1.Ordnung
hat die Lösung
Eine homogene lineare RG 2. Ordnung hat
- bei
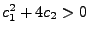 die Reelle Lösung:
wobei
die Reelle Lösung:
wobei
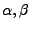 die zwei (verschiedenen) Lösungen der Gleichung
die zwei (verschiedenen) Lösungen der Gleichung
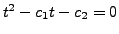 sind
und
sind
und
- bei
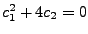 die Reelle Lösung:
die Reelle Lösung:
- bei
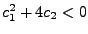 die komplexe Lösungen. Formeln siehe bei
die komplexe Lösungen. Formeln siehe bei
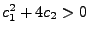 .
.
Fibonacci-Folge
Die Fibonacci-Folge
hat die Lösung:





Next: Erzeugende Funktionen
Up: Rekursionen
Previous: Rekursionen
Contents
Index
Marco Möller 17:26:01 24.10.2005