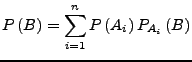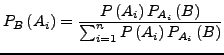Next: Unabhängigkeit und Wahrscheinlichkeitsverteilung
Up: Wahrscheinlichkeitstheorie
Previous: Wahrscheinlichkeitstheorie
Contents
Index
Subsections
Diskrete Wahrscheinlichkeitstheorie
Sei 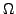 eine höchstens abzählbare Menge (d.h. es gibt eine surjektive
Abbildung
eine höchstens abzählbare Menge (d.h. es gibt eine surjektive
Abbildung
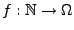 ) und sei
) und sei
![$ P:\mathcal{P}\left(\Omega\right)\rightarrow\left[0,1\right]$](img314.png) (
(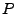 von Probability = Wahrscheinlichkeit) eine Abbildung
mit den Eigenschaften:
von Probability = Wahrscheinlichkeit) eine Abbildung
mit den Eigenschaften:
-
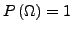
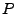 ist additiv auf disjunkten Mengen:
ist additiv auf disjunkten Mengen:
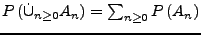
Dann heißt
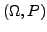 ein diskreter Wahrscheinlichkeitsraum
(endlicher Wahrscheinlichkeitsraum,
falls
ein diskreter Wahrscheinlichkeitsraum
(endlicher Wahrscheinlichkeitsraum,
falls 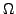 endlich), und
endlich), und 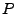 heißt die Wahrscheinlichkeitsverteilung
auf
heißt die Wahrscheinlichkeitsverteilung
auf 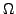 .
.
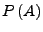 nennen wir die Wahrscheinlichkeit
von
nennen wir die Wahrscheinlichkeit
von 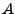 .
.
Wir nennen
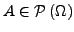 ein Ereignis
in
ein Ereignis
in 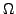 , und falls
, und falls
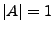 , Elementarereignis.
, Elementarereignis.
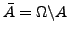 heißt Gegenereignis
zu
heißt Gegenereignis
zu 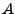 .
.
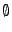 heißt unmögliches Ereignis
und
heißt unmögliches Ereignis
und 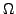 sicheres Ereignis.
sicheres Ereignis.
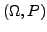 heißt Laplacescher Wahrscheinlichkeitsraum,
falls
heißt Laplacescher Wahrscheinlichkeitsraum,
falls
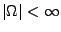 und
und
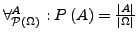 .
.
- insbesondere
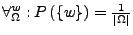
Sei
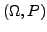 ein diskreter W-Raum,
ein diskreter W-Raum,
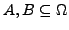 ,
,
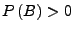 .
.
heißt bedingte W-keit von 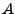 bezüglich
bezüglich 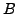 (d.h. die W-keit von
(d.h. die W-keit von
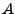 , falls man schon weiß, dass
, falls man schon weiß, dass 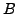 erfüllt ist).
erfüllt ist).
-
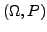 ein diskreter W-Raum,
ein diskreter W-Raum,
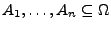 ,
,
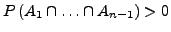 .
.
Formel von der vollständigen Wahrscheinlichkeit
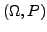 ein diskreter W-Raum,
ein diskreter W-Raum,
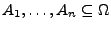 mit
mit
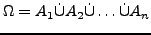 ,
P
,
P
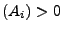 ,
,
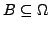 mit
mit
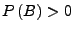 .
Dann:
.
Dann:
- Für
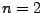 :
:
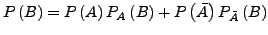





Next: Unabhängigkeit und Wahrscheinlichkeitsverteilung
Up: Wahrscheinlichkeitstheorie
Previous: Wahrscheinlichkeitstheorie
Contents
Index
Marco Möller 17:26:01 24.10.2005
![]() eine höchstens abzählbare Menge (d.h. es gibt eine surjektive
Abbildung
eine höchstens abzählbare Menge (d.h. es gibt eine surjektive
Abbildung
![]() ) und sei
) und sei
![]() (
(![]() von Probability = Wahrscheinlichkeit) eine Abbildung
mit den Eigenschaften:
von Probability = Wahrscheinlichkeit) eine Abbildung
mit den Eigenschaften:
![]() ein Ereignis
in
ein Ereignis
in ![]() , und falls
, und falls
![]() , Elementarereignis.
, Elementarereignis.
![]() heißt unmögliches Ereignis
und
heißt unmögliches Ereignis
und ![]() sicheres Ereignis.
sicheres Ereignis.
![]() heißt Laplacescher Wahrscheinlichkeitsraum,
falls
heißt Laplacescher Wahrscheinlichkeitsraum,
falls
![]() und
und
![]() .
.
![]() ein diskreter W-Raum,
ein diskreter W-Raum,
![]() ,
,
![]() .
.
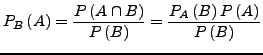
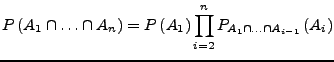
![]() ein diskreter W-Raum,
ein diskreter W-Raum,
![]() mit
mit
![]() ,
P
,
P
![]() ,
,
![]() mit
mit
![]() .
Dann:
.
Dann: