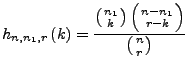Next: Erwartungswert und Varianz
Up: Wahrscheinlichkeitstheorie
Previous: Diskrete Wahrscheinlichkeitstheorie
Contents
Index
Subsections
Unabhängigkeit und Wahrscheinlichkeitsverteilung
Sei
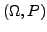 ein diskreter W-Raum. Wir nennen zwei
Ereignisse
ein diskreter W-Raum. Wir nennen zwei
Ereignisse
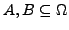 unabhängig voneinander,
falls
unabhängig voneinander,
falls
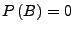 oder
oder
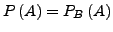 .
Diese Aussage ist Äquivalent zu
.
Diese Aussage ist Äquivalent zu
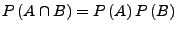 .
.
Allgemein heißen
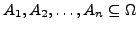 unabhängig
voneinander, falls für alle
unabhängig
voneinander, falls für alle
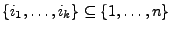 mit
mit 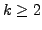 gilt:
gilt:
Eine Verteilungsfunktion
![$ P^{n}:\Omega^{n}\rightarrow\left[0,1\right]$](img352.png) die jedem
die jedem
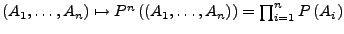 Tupel von Ereignissen eine Wahrscheinlichkeit zuordnet.
Tupel von Ereignissen eine Wahrscheinlichkeit zuordnet.
Binomialverteilung
Wir betrachten
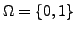 mit
mit
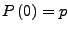 und
und
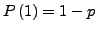 . Die Binomialverteilung
. Die Binomialverteilung
gibt an, wie groß die Wahrscheinlichkeit ist, das bei 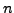 -maligen
Wiederholen genau
-maligen
Wiederholen genau 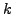 -mal ein Ereigniss mit der Wahrscheinlichkeit
-mal ein Ereigniss mit der Wahrscheinlichkeit
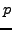 auftritt.
auftritt.
- z.B. 10-maliger Münzwurf. Wie groß ist die Wahrscheinlichkeit, das
genau 7 Mal Zahl kommt:
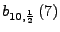
- ist bezüglich verschiedenen
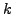 disjunkt
disjunkt
-
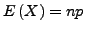
-
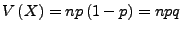
Hypergeometrische Verteilung
Situation: Urne mit 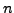 Kugeln, davon seien
Kugeln, davon seien 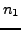 ausgezeichnet.
Wir ziehen
ausgezeichnet.
Wir ziehen 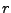 Kugeln
Kugeln
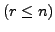 . Wie viele dieser
. Wie viele dieser 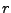 Kugeln gehören zu den
Kugeln gehören zu den 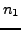 ausgezeichnet?
ausgezeichnet?
- ist bezüglich verschiedenen
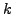 disjunkt
disjunkt
- Bei großen Zahlen
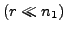 lässt sich
lässt sich
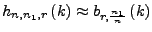 annähern
annähern
-





Next: Erwartungswert und Varianz
Up: Wahrscheinlichkeitstheorie
Previous: Diskrete Wahrscheinlichkeitstheorie
Contents
Index
Marco Möller 17:26:01 24.10.2005
![]() ein diskreter W-Raum. Wir nennen zwei
Ereignisse
ein diskreter W-Raum. Wir nennen zwei
Ereignisse
![]() unabhängig voneinander,
falls
unabhängig voneinander,
falls
![]() oder
oder
![]() .
Diese Aussage ist Äquivalent zu
.
Diese Aussage ist Äquivalent zu
![]() .
.
![]() unabhängig
voneinander, falls für alle
unabhängig
voneinander, falls für alle
![]() mit
mit ![]() gilt:
gilt:
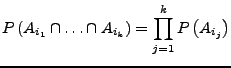
![]() die jedem
die jedem
![]() Tupel von Ereignissen eine Wahrscheinlichkeit zuordnet.
Tupel von Ereignissen eine Wahrscheinlichkeit zuordnet.
![]() mit
mit
![]() und
und
![]() . Die Binomialverteilung
. Die Binomialverteilung
![]() Kugeln, davon seien
Kugeln, davon seien ![]() ausgezeichnet.
Wir ziehen
ausgezeichnet.
Wir ziehen ![]() Kugeln
Kugeln
![]() . Wie viele dieser
. Wie viele dieser ![]() Kugeln gehören zu den
Kugeln gehören zu den ![]() ausgezeichnet?
ausgezeichnet?