




Next: Gesteuerte Quellen I.111
Up: Widerstandsnetzwerk I.26
Previous: Überlagerungssatz / Superpositionsprinzip (nach
Contents
Index
Subsections
Aufstellen eines linearen Gleichungssystems
I.84
Durch das Aufstellen aller über ein Netzwerk bekannten Beziehungen,
erhält man ein Gleichungssystem, das sich mit Hilfe der Mathematik
mehr oder weniger leicht lösen lässt. Allgemein benötigt man für jede
Unbekannte in einem Netz 1 Gleichung. Um hier nicht aus Versehen linear
abhängige aufzustellen, nutzt man folgende Regeln.
- Aus den Umläufen kann man Gleichungen beziehen. Allerdings sollten
nur die Maschen genutzt werden, da so keine Größe vergessen, und auch
keine lin. Abhängigkeit entstehen kann. Aus einer Schaltung mit
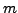 Maschen
erhält man
Maschen
erhält man 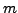 Umlaufgleichungen (siehe 3.2).
Umlaufgleichungen (siehe 3.2).
- Aus den Knoten kann man Gleichungen beziehen. Allerdings sind bei
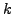 Knoten nur
Knoten nur 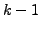 linear unabhängige. Welche das sind, spielt
keine Rolle.
linear unabhängige. Welche das sind, spielt
keine Rolle.
- An jedem Widerstand lässt sich die Beziehung
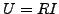 bzw.
bzw.
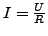 aufstellen.
aufstellen.
In dem so erstellen Gleichungssystem sind enorm viele Gleichungen
vorhanden. Von vornherein einfacher wird es, in dem man in den Umlaufgleichungen
direkt anstelle der Spannungen das Produkt aus Widerstand und Strom
schreibt.
Umlaufanalyse I.91
Bei der Umlaufanalyse handelt es sich um ein Verfahren, um möglichst
einfach ein lineares Gleichungssystem mit
wenig Unbekannten zu erhalten. Um ein Gleichungssystem der Gestalt
(Indizes absichtlich so, da die Matrix spiegelsymetrisch auf der Haupt-Diagonale
ist) zu erhalten, muss man folgendes Schema anwenden:
- Stromquellen wenn möglich in Spannungsquellen transformieren.
- Alle Leitwerte (wenn vorhanden) in Widerstände umrechnen.
- Für das Netz einen vollständigen Baum auswählen.
Dabei folgendes beachten:
- Alle Stromquellen müssen in Verbindungszweige liegen, alle Spannungsquellen
sollten.
- gesuchte Ströme möglichst in Verbindungszweige legen
- Baum so wählen das möglichst einfache Umläufe entstehen (möglichst
kurz) (möglichst Sternförmig)
- Einen Baumzweig sollten sich möglichst wenig Umläufe ``teilen''
- Über Stromquellen einen Spannungspfeil eintragen
- In den Verbindungszweigen Zählpfeile (für Stromrichtung) eintragen
- In den Stromvektor alle Ströme aus Verbindungszweigen
zuordnen
- Jedem Strom aus Verbindungszweig einen Umlauf, der sich nur über Baumzweige
schließt, zuordnen. Richtung wie Zählpfeil.
- Für jeden Umlauf eine Zeile des obigen Gleichungssystems aufstellen:
- Diagonalelement der Widerstandmatrix (
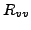 ) ist die Summe aller
Widerstände im jeweiligen Umlauf
) ist die Summe aller
Widerstände im jeweiligen Umlauf 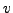 .
.
Vorzeichen: +
- Andere Matrixelemente (
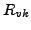 ) sind die Kopplungswiderstände
zwischen den Umläufen. Der Umlauf
) sind die Kopplungswiderstände
zwischen den Umläufen. Der Umlauf 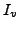 hat in z.B. in der k-ten
Spalte die Summe aller Widerstände die der Umlauf k und v gemeinsam
haben stehen.
hat in z.B. in der k-ten
Spalte die Summe aller Widerstände die der Umlauf k und v gemeinsam
haben stehen.
Vorzeichen: + für im Baum gleichgerichtete Umläufe, - für entgegen
gerichtete.
- Das Element des Spannungsvektors wird aus
der Summe aller Quellspannungen des Umlaufes gebildet.
Vorzeichen: + wenn Spannungszählpfeil gegen den Umlaufsinn, - wenn
im Umlaufsinn.
- Überprüfen, ob die Elemente der Matrix wirklich Spiegelsymetrisch
zu der Diagonale (Diagonale von Oben Links nach Unten Rechts) sind.
Wenn nicht, alles von vorn...
- Wenn im Netzwerk noch Stromquellen enthalten waren, die Matrix für
jede dieser Quellen wie folgt vereinfachen:
- Die Zeile mit dem Umlauf über die Stromquelle streichen.
- In allen anderen Zeilen die zur Stromquelle zugehörige Spalte streichen.
Wert der gestrichenen Zellen mit umgekehrten Vorzeichen und Multipliziert
mit dem Stomquellenstrom in die entsprechenden Zellen im Spannungsvektor
eintragen (jeweils in die gleiche Zeile).
- Gleichungssystem Lösen
- Alle nun noch nicht bekannten Größen mit Hilfe der Kirchhoffschen
Gleichungen (siehe Krichhoffschen-Gleichungen) und des Ohmschen
Gesetzes errechnen.
Knotenanalyse I.101
Bei der Knotenanalyse handelt es sich um ein Verfahren, um möglichst
einfach ein lineares Gleichungssystem mit wenig Unbekannten zu erhalten.
Um ein Gleichungssystem der Gestalt
(Indizes absichtlich so, da die Matrix spiegelsymetrisch auf der Haupt-Diagonale
ist) zu erhalten, muss man folgendes Schema anwenden:
- Spannungsquellen wenn möglich in Stromquellen Transformieren.
- Alle Widerstände (wenn vorhanden) in Leitwerte umrechnen.
- Für das Netz einen Sternförmigen vollständigen Baum
auswählen. Dabei folgendes beachten:
- Wenn nicht möglich, das Netzwerk entsprechend um Leitwerte mit
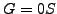 ergänzen.
ergänzen.
- gesuchte Spannungen möglichst in Baumzweige legen
- Alle Spannungsquellen müssen in Baumzweigen liegen
- Zählpfeile der unabhängigen Spannungen längs der Baumzweige in Richtung
des Bezugsknotens (Mittelpunkt) eintragen
- In den Spannungsvektor alle Spannungen aus den Baumzweigen eintragen
- Für jeden Knoten (außer dem mittlerem Bezugsknoten) eine Zeile des
Gleichungssystems aufstellen:
- Diagonalelement der Leitwertmatix (
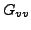 ) ist die Summe aller
Leitwerte (entspricht-Parallelschaltung) die im jeweiligen Knoten
v zusammentreffen.
) ist die Summe aller
Leitwerte (entspricht-Parallelschaltung) die im jeweiligen Knoten
v zusammentreffen.
Vorzeichen: +
- Andere Matrixelemente (
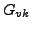 ) sind die Summe der Kopplungsleitwerte
zwischen den Knoten v und k.
) sind die Summe der Kopplungsleitwerte
zwischen den Knoten v und k.
Vorzeichen: -
- Das Element des Stromvektors wird aus der Summe aller Quellströme
die an den jeweiligen Knoten angeschlossen sind gebildet.
Vorzeichen: + wenn der Strom in den Knoten hinein fließt, - wenn heraus
fließt.
- Überprüfen, ob die Elemente der Matrix wirklich Spiegelsymetrisch
zu der Diagonale (Diagonale von Oben Links nach Unten Rechts) sind.
Wenn nicht, alles von vorn...
- Wenn im Netzwerk noch Spannungsquellen enthalten waren, die Matrix
für jede dieser Quellen wie folgt vereinfachen:
- Die Zeile mit dem Zweig der die Spannungsquelle enthält streichen.
- In allen anderen Zeilen die zur Spannungsquelle zugehörige Spalte
streichen. Wert der gestrichenen Zellen mit umgekehrten Vorzeichen
und Multipliziert mit der Spannungsquellenspannung in die entsprechenden
Zellen im Stromvektor eintragen (jeweils in die gleiche Zeile).
- Gleichungssystem Lösen
- Alle nun noch nicht bekannten Größen mit Hilfe der Kirchhoffschen
Gleichungen (siehe Krichhoffschen-Gleichungen) und des Ohmschen
Gesetzes errechnen.
Vergleich von Knoten-
und Umlaufanalyse I.108
In Tabelle Tabel:VergleichKontenUmlauf kann man ersehen, wie
groß ein Gleichungssystem bei der jeweiligen
Analysemethode werden würde. Man muss allerdings auch den Aufwand
zum Erstellen eines solchen Gleichungssystems mit in die Betrachtung
mit einbeziehen.





Next: Gesteuerte Quellen I.111
Up: Widerstandsnetzwerk I.26
Previous: Überlagerungssatz / Superpositionsprinzip (nach
Contents
Index
Marco Möller 17:32:09 24.10.2005
![\begin{displaymath}
\begin{array}{c}
\textrm{Umlauf mit }I_{1}:\\
.\\
\textrm{...
... U_{q1}\\
.\\
\pm U_{qv}\\
.\\
\pm U_{qn}\end{array}\right]\end{displaymath}](img169.png)
![\begin{displaymath}
\begin{array}{c}
\textrm{K. 1}:\\
.\\
\textrm{K. v}:\\
.\...
...q1}\\
.\\
\pm I_{qv}\\
.\\
\pm I_{q(k-1)}\end{array}\right]\end{displaymath}](img173.png)