




Next: Der Lösungsraum I.220
Up: Formelsammlung Mathe I/II für
Previous: Lineare Abbildungen und Matrizen
Contents
Index
Lineare Gleichungssysteme
I.220
Sei
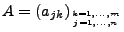 eine
eine 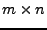 -Matrix mit Elementen aus
-Matrix mit Elementen aus
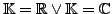 und
und
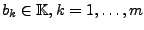 .
.
Das System
heißt lineares Gleichungssystem (LGS) mit 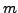 Gleichungen
und
Gleichungen
und 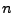 Unbekannten.
Unbekannten.
Jedes 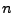 -Tupel (Vektor)
-Tupel (Vektor)
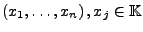 ,
das alle Gleichungen löst, heißt Lösung des Systems. Die Gesamtheit
aller Lösungen heißt Lösungsraum.
,
das alle Gleichungen löst, heißt Lösung des Systems. Die Gesamtheit
aller Lösungen heißt Lösungsraum.
Subsections
Marco Möller 17:42:11 24.10.2005
![]() eine
eine ![]() -Matrix mit Elementen aus
-Matrix mit Elementen aus
![]() und
und
![]() .
.
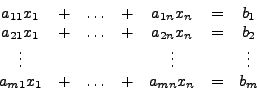
![]() -Tupel (Vektor)
-Tupel (Vektor)
![]() ,
das alle Gleichungen löst, heißt Lösung des Systems. Die Gesamtheit
aller Lösungen heißt Lösungsraum.
,
das alle Gleichungen löst, heißt Lösung des Systems. Die Gesamtheit
aller Lösungen heißt Lösungsraum.