




Next: Lösen mittels Inversen
Up: Lineare Gleichungssysteme I.220
Previous: Lineare Gleichungssysteme I.220
Contents
Index
Subsections
Der Lösungsraum I.220
Der Lösungsraum des homogenen Systems
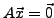 mit einer
mit einer 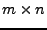 -Matrix
-Matrix  , stellt einen Untervektorraum
der Dimension
, stellt einen Untervektorraum
der Dimension
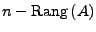 von
von
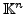 dar.
dar.
- Jedes homogene Gleichungssystem ist lösbar
- Ist
 quadratisch und regulär, so hat der Lösungsraum die Dimension
0, besteht also nur aus dem Nullvektor
quadratisch und regulär, so hat der Lösungsraum die Dimension
0, besteht also nur aus dem Nullvektor 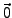 .
.
Erweiterte Matrix I.224
Die
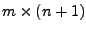 -Matrix
-Matrix
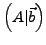 heißt
erweiterte Matrix des LGS.
heißt
erweiterte Matrix des LGS.
Rangkriterium I.224
Das inhomogene LGS
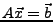 ist
genau dann lösbar, falls
ist
genau dann lösbar, falls
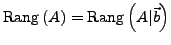
- Wenn
 quadratisch und regulär ist auch inhomogenes System lösbar,
mit einer eindeutigen Lösung.
quadratisch und regulär ist auch inhomogenes System lösbar,
mit einer eindeutigen Lösung.
- Allgemeiner Fall: Sei
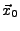 eine feste Lösung von
eine feste Lösung von
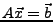 und
und 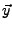 eine Lösung des Systems
eine Lösung des Systems
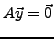 . Dann ist
. Dann ist
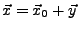 eine beliebige Lösung von
eine beliebige Lösung von
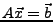 .
.
Basiswechsel
Die lineare Abbildung
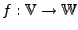 mit der
Abbildungsmatrize
mit der
Abbildungsmatrize
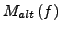 ist mit
ist mit
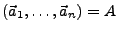 als Basis von
als Basis von
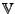 und
und
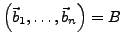 als Basis von
als Basis von
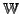 gegeben. Um sie nun in die neuen Basen
gegeben. Um sie nun in die neuen Basen
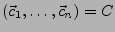 von
von
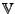 und
und
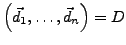 und von
und von
 zu überführen, wende folgende Gleichung an.
zu überführen, wende folgende Gleichung an.
- Für den Sonderfall das
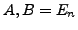 und
und 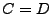 gilt:
gilt:
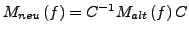
- Für weiteres siehe sub:Basiswechsel ohne Matrix





Next: Lösen mittels Inversen
Up: Lineare Gleichungssysteme I.220
Previous: Lineare Gleichungssysteme I.220
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() mit einer
mit einer ![]() -Matrix
-Matrix ![]() , stellt einen Untervektorraum
der Dimension
, stellt einen Untervektorraum
der Dimension
![]() von
von
![]() dar.
dar.
![]() -Matrix
-Matrix
![]() heißt
erweiterte Matrix des LGS.
heißt
erweiterte Matrix des LGS.
![]() ist
genau dann lösbar, falls
ist
genau dann lösbar, falls
![]()
![]() mit der
Abbildungsmatrize
mit der
Abbildungsmatrize
![]() ist mit
ist mit
![]() als Basis von
als Basis von
![]() und
und
![]() als Basis von
als Basis von
![]() gegeben. Um sie nun in die neuen Basen
gegeben. Um sie nun in die neuen Basen
![]() von
von
![]() und
und
![]() und von
und von
![]() zu überführen, wende folgende Gleichung an.
zu überführen, wende folgende Gleichung an.