




Next: Determinanten I.241
Up: Lineare Gleichungssysteme I.220
Previous: Lösen mittels Inversen
Contents
Index
Subsections
Der Gaußsche Algorithmus I.227
Da Zeilenoperationen (Tauschen / Multiplizieren / Addieren) in der
erweiterten Matrix
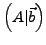 eines linearen Gleichungssystems
eines linearen Gleichungssystems
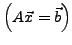 den Lösungsraum nicht verändern,
lassen diese sich zum Lösen des Gleichungssystems verwenden. Man kann
dabei nach dem folgenden (Gaußschen) Algorithmus vorgehen:
den Lösungsraum nicht verändern,
lassen diese sich zum Lösen des Gleichungssystems verwenden. Man kann
dabei nach dem folgenden (Gaußschen) Algorithmus vorgehen:
- Vertausche Zeilen so, das oben Links etwas von 0 verschiedenes
steht (
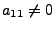 ). Falls erste Spalte
). Falls erste Spalte 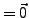
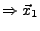 beliebig, streichen der 1. Spalte
beliebig, streichen der 1. Spalte
- Räume Spalte unterhalb von
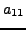 aus, durch Addition von
aus, durch Addition von
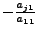 (
(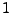 .
Zeile) auf
.
Zeile) auf 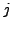 -te Zeile
-te Zeile
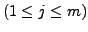
- Wenn die akt. Untermatrix mehr als 1. Zeile hat, betrachte Untermatrix,
in der die 1.Spalte und die 1.Zeile fehlen, und mache bei 1. weiter.
- Testen der Rangbedingung für Lösbarkeit. Wenn
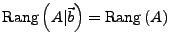 ist es wie folgt lösbar
ist es wie folgt lösbar
- Löse LGS von unten nach Oben auf
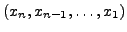
- Unbekannte zugehörig zu den Nullspalten können frei gewählt werden.
- Unbekannte zu den Nullzeiten werden als Parameter gewählt
Man führe den Gauß-Algorithmus für die Matrix
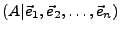 aus. Dabei muss das System mittels Zeilenoperationen in die Gestalt
aus. Dabei muss das System mittels Zeilenoperationen in die Gestalt
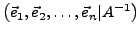 gebracht werden. Auf der Rechten Seite lässt sich nun die Inverse
Matrix ablesen.
gebracht werden. Auf der Rechten Seite lässt sich nun die Inverse
Matrix ablesen.
Es ist auch möglich, ausschließlich mit Spalten Operationen
anstatt Zeilenoperationen zu arbeiten.





Next: Determinanten I.241
Up: Lineare Gleichungssysteme I.220
Previous: Lösen mittels Inversen
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() eines linearen Gleichungssystems
eines linearen Gleichungssystems
![]() den Lösungsraum nicht verändern,
lassen diese sich zum Lösen des Gleichungssystems verwenden. Man kann
dabei nach dem folgenden (Gaußschen) Algorithmus vorgehen:
den Lösungsraum nicht verändern,
lassen diese sich zum Lösen des Gleichungssystems verwenden. Man kann
dabei nach dem folgenden (Gaußschen) Algorithmus vorgehen:
![]() aus. Dabei muss das System mittels Zeilenoperationen in die Gestalt
aus. Dabei muss das System mittels Zeilenoperationen in die Gestalt
![]() gebracht werden. Auf der Rechten Seite lässt sich nun die Inverse
Matrix ablesen.
gebracht werden. Auf der Rechten Seite lässt sich nun die Inverse
Matrix ablesen.