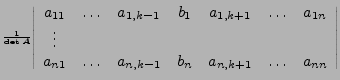Next: Eigenwerte I.266
Up: Determinanten I.241
Previous: Entwicklung nach einer Zeile/Spalte
Contents
Index
Subsections
Sei
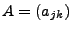 eine
eine 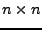 -Matrix mit
-Matrix mit
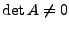 .
Dann hat die inverse Matrix die Gestalt:
.
Dann hat die inverse Matrix die Gestalt:
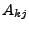 ist Adjunkte Matrix (Achtung: Indizes vertauscht (Transponiert))
ist Adjunkte Matrix (Achtung: Indizes vertauscht (Transponiert))
Carmersche Regel I.261
Sei
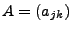 eine reguläre
eine reguläre 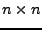 -Matrix. Dann
hat das lineare Gleichungssystem
-Matrix. Dann
hat das lineare Gleichungssystem
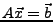 die Lösung
die Lösung
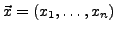 gegeben durch
gegeben durch
- Teile die Determinante von
 mit
mit 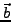 in der
in der 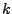 -ten Spalte
durch die Determinante von
-ten Spalte
durch die Determinante von  und du erhältst die Lösung für
und du erhältst die Lösung für 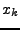
Marco Möller 17:42:11 24.10.2005
![]() eine
eine ![]() -Matrix mit
-Matrix mit
![]() .
Dann hat die inverse Matrix die Gestalt:
.
Dann hat die inverse Matrix die Gestalt:
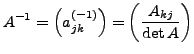
![]() eine reguläre
eine reguläre ![]() -Matrix. Dann
hat das lineare Gleichungssystem
-Matrix. Dann
hat das lineare Gleichungssystem
![]() die Lösung
die Lösung
![]() gegeben durch
gegeben durch