




Next: Drehung im und Quadriken
Up: Eigenwerte I.266
Previous: Eigenvektoren I.272
Contents
Index
Subsections
Eine lineare Abbildung
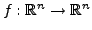 heißt orthogonal, wenn sie das Skalarprodukt
unverändert lässt, also
heißt orthogonal, wenn sie das Skalarprodukt
unverändert lässt, also
Unitäre Matrizen I.284
Eine 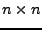 -Matrix mit Einträgen aus
-Matrix mit Einträgen aus
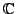 heißt unitär,
wenn
heißt unitär,
wenn
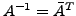 .
.
- Liegen alle Einträge in
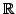 , so gilt
, so gilt  orthogonal (
orthogonal (
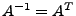 )
)
- Zeilenvektoren und Spaltenvektoren von
 bilden jeweils ein Orthonormalsystem.
bilden jeweils ein Orthonormalsystem.
-
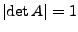
- Für alle Eigenwerte
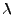 von
von  gilt
gilt
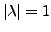 .
.
- Die Eigenvektoren zu zwei unterschiedlichen Eigenwerten sind orthogonal
zueinander, also
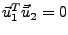 .
.
Eine 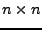 -Matrix mit Einträgen aus
-Matrix mit Einträgen aus
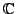 heißt hermitesch,
wenn
heißt hermitesch,
wenn
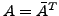 .
.
- Liegen alle Einträge in
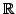 , so ist
, so ist  symmetrisch (
symmetrisch (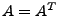 )
)
- Alle Eigenwerte von
 sind reell
sind reell
- Die Eigenvektoren zu zwei unterschiedlichen Eigenwerten sind orthogonal
zueinander, also
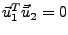 .
.
- Für jeden Eigenwert stimmen geometrische und die algebraische Vielfachheit
überein.
 ist diagonalähnlich
ist diagonalähnlich
- Zu jeder hermiteschen (symmetrischen) Matrix
 gibt es eine unitäre
(orthogonale) Matrix
gibt es eine unitäre
(orthogonale) Matrix 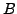 , mit der
, mit der  in eine reelle Diagonalmatrix
in eine reelle Diagonalmatrix
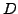 überführt werden kann.
überführt werden kann.
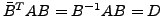





Next: Drehung im und Quadriken
Up: Eigenwerte I.266
Previous: Eigenvektoren I.272
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() heißt orthogonal, wenn sie das Skalarprodukt
unverändert lässt, also
heißt orthogonal, wenn sie das Skalarprodukt
unverändert lässt, also
![]() -Matrix mit Einträgen aus
-Matrix mit Einträgen aus
![]() heißt unitär,
wenn
heißt unitär,
wenn
![]() .
.
![]() -Matrix mit Einträgen aus
-Matrix mit Einträgen aus
![]() heißt hermitesch,
wenn
heißt hermitesch,
wenn
![]() .
.