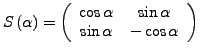Next: Überführen von allgemeine Quadriken
Up: Drehung im und Quadriken
Previous: Drehung im und Quadriken
Contents
Index
Subsections
Ellipse
Ortslinie aller Punkte, die von zwei vorgegebenen Punkten (Brennpunkten)
feste Abstandssumme haben. Die Normalform der Ellipsengleichng lautet
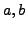 nennen sich Halbachsen (Schnittpunkt
der Ellipse mit den Koordinatenachsen)
nennen sich Halbachsen (Schnittpunkt
der Ellipse mit den Koordinatenachsen)
-
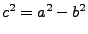
- Brennpunkte in
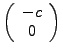 ,
,
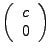
- Exzentrizität von einer Ellipse
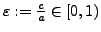
- Spezialfall
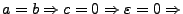 Kreis
mit Radius
Kreis
mit Radius 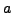
- keine Asymptoten
- Entsteht z.B. durch Kegelschnitt mit Schnittebene die nur einen der
beiden Kegel schneidet.
Parabel
Ortslinie aller Punkte, die von einem vorgegebenen Punkt 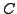 (Brennpunkt)
selben Abstand wie von einer vorgegebenen Geraden
(Brennpunkt)
selben Abstand wie von einer vorgegebenen Geraden 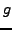 haben.
haben.
- Scheitel der Parabel (Extremstelle) bei
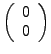
- Brennpunkt bei
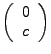
- Exzentrizität von einer Parabel
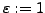
- keine Asymptoten
- Entsteht z.B. durch Kegelschnitt mit Schnittebene parallel zu Kegelkanten
Hyperbel
Ortslinie aller Punkte die zu zwei vorgegebenen Punkten (Brennpunkte)
festen Betrag der Abstandsdifferenz haben.
- diese Formel für Hyperbel die nach links/rechts geöffnet ist
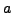 Schnitt der Hyperbelzweige mit der
Schnitt der Hyperbelzweige mit der 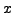 -Achse
-Achse
-
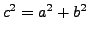
- Brennpunkte bei
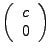 ,
,
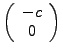
- Exzentrizität von einer Hyperbel
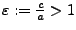
- nach oben/unten geöffnet mit
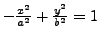
- Asymptoten
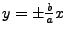
- Entsteht z.B. durch Kegelschnitt mit Schnittebene die durch oberen
und unteren Kegel geht
Drehung in
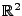
Ein Punkt
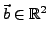 lässt sich mit Hilfe der Matrize
lässt sich mit Hilfe der Matrize
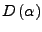 um den Winkel
um den Winkel 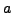 drehen.
drehen.
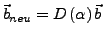
-
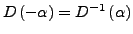
- Eigenwerte von
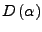 :
:
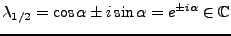
- ist eine orthogonale Abbildung
Spiegelung in
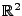
Ein Punkt
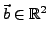 lässt sich mit Hilfe der Matrize
lässt sich mit Hilfe der Matrize
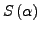 um eine Gerade die den Winkel
um eine Gerade die den Winkel 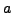 zur
zur 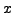 Achse einnimmt spiegeln.
Achse einnimmt spiegeln.
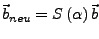
- ist eine orthogonale Abbildung





Next: Überführen von allgemeine Quadriken
Up: Drehung im und Quadriken
Previous: Drehung im und Quadriken
Contents
Index
Marco Möller 17:42:11 24.10.2005
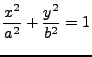
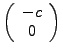 ,
,
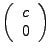
![]() (Brennpunkt)
selben Abstand wie von einer vorgegebenen Geraden
(Brennpunkt)
selben Abstand wie von einer vorgegebenen Geraden ![]() haben.
haben.
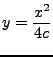
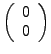
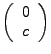
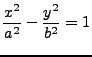
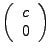 ,
,
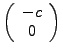
![]() lässt sich mit Hilfe der Matrize
lässt sich mit Hilfe der Matrize
![]() um den Winkel
um den Winkel ![]() drehen.
drehen.
![]()
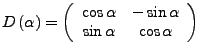
![]() lässt sich mit Hilfe der Matrize
lässt sich mit Hilfe der Matrize
![]() um eine Gerade die den Winkel
um eine Gerade die den Winkel ![]() zur
zur ![]() Achse einnimmt spiegeln.
Achse einnimmt spiegeln.
![]()