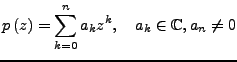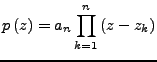Next: Vietascher Wurzelsatz I.72
Up: Komplexe Zahlen I.44
Previous: Polarkoordinaten I.60
Contents
Index
Fundamentalsatz der Algebra
I.71
Zu jedem Polynom vom Grad 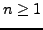
gibt es 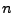 (nicht zwangsläufig unterschiedliche) komplexe Zahlen
(nicht zwangsläufig unterschiedliche) komplexe Zahlen
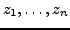 , so dass
für alle
, so dass
für alle
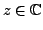 gilt.
gilt.
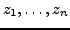 sind die Nullstellen
des Polynoms. Diese Umformung nennt sich Faktorisieren
in Linearfaktoren.
sind die Nullstellen
des Polynoms. Diese Umformung nennt sich Faktorisieren
in Linearfaktoren.
Es lässt sich auch nur ein Linearfaktor abspalten. Dann erhält man
einen Linearfaktor und ein Restpolynom vom einem
um 1 verringerten Grad.
Marco Möller 17:42:11 24.10.2005