




Next: Reihen II.22
Up: Folgen II.3
Previous: Konvergenzkriterien
Contents
Index
Subsections
- Im Allgemeinen lassen sich zwei Grenzwertbildungen nicht in der Reihenfolge
vertauschen!
Unbestimmte Formen
Unbestimmte Formen siehe Tabelle unbestFormen. Diese lassen
sich alle bis auf
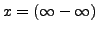 lösen mit Hilfe
der Regeln von de l'Hospital (siehe
sub:Regeln-de-l-Hospital).
lösen mit Hilfe
der Regeln von de l'Hospital (siehe
sub:Regeln-de-l-Hospital).
Marco Möller 17:42:11 24.10.2005
![]() lösen mit Hilfe
der Regeln von de l'Hospital (siehe
sub:Regeln-de-l-Hospital).
lösen mit Hilfe
der Regeln von de l'Hospital (siehe
sub:Regeln-de-l-Hospital).