




Next: absolut / bedingt konvergent
Up: Reihen II.22
Previous: Reihen II.22
Contents
Index
Subsections
Konvergenz II.22
Die Reihen
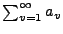 und
und
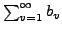 seien konvergent, dann gilt: II.23
seien konvergent, dann gilt: II.23
Wenn eine Reihe
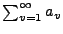 konvergiert, dann ist
konvergiert, dann ist
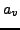 eine Nullfolge (
eine Nullfolge (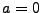 ) II.24
) II.24
- Cauchy-Konvergenzkriterium für Reihen
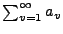 konvergent, wenn
konvergent, wenn
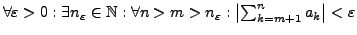
Marco Möller 17:42:11 24.10.2005
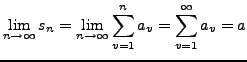
![]() und
und
![]() seien konvergent, dann gilt: II.23
seien konvergent, dann gilt: II.23
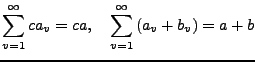
![]() konvergiert, dann ist
konvergiert, dann ist
![]() eine Nullfolge (
eine Nullfolge (![]() ) II.24
) II.24