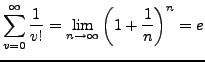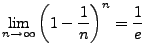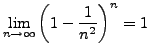Next: Funktionsfolgen und Funktionsreihen
Up: Reihen II.22
Previous: Konvergenzkriterien II.168
Contents
Index
Subsections
Besondere Reihen
- Weitere Reihen siehe sub:wichtige-Reihen-II.154
- geometrische Reihe II.25
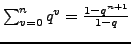
(konvergent wenn
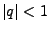 )
)
- harmonische Reihe II.27
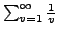 (divergent)
(divergent)
- alternierende harmonische Reihe
II.28
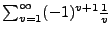 (konvergent)
(konvergent)
-
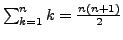
-
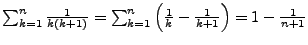
-
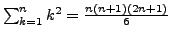
-
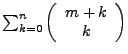 =
=
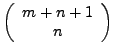
-
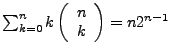
Eulersche Zahl 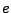 II.34
II.34
Folgende Reihen sind absolut Konvergent gegen 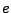 .
.
Marco Möller 17:42:11 24.10.2005
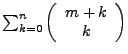 =
=
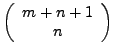
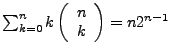
![]() .
.