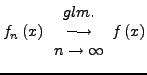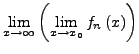Next: Vertauschen von Grenzwerten
Up: Funktionsfolgen und Funktionsreihen
Previous: Funktionsfolgen und Funktionsreihen
Contents
Index
Subsections
Punktweise Konvergenz II.178
Eine Folge von Funktionen
![$ \left(f_{n}\right)_{n=1}^{\infty},\; f_{n}:\left[a,b\right]\rightarrow\mathbb{R}$](img339.png) konvergiert punktweise, wenn
konvergiert punktweise, wenn
![$ \forall_{\left[a,b\right]}^{x}:\left(f_{n}\left(x\right)\right)_{n=1}^{\infty}$](img340.png) konvergiert. Die durch
konvergiert. Die durch
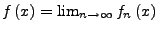 in
in
![$ \left[a,b\right]$](img342.png) erklärte Funktion heißt Grenzfunktion.
erklärte Funktion heißt Grenzfunktion.
Man schreibt
Gleichmäßige Konvergenz II.178
Die Funktion
![$ f_{n}:\left[a,b\right]\rightarrow\mathbb{R},\;\left(n\geq1\right)$](img344.png) ,
und
,
und
![$ f:\left[a,b\right]\rightarrow\mathbb{R}$](img345.png) seien beschränkt. Die
Folge
seien beschränkt. Die
Folge
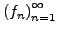 konvergiert gleichmäßig
gegen die Grenzfunktion
konvergiert gleichmäßig
gegen die Grenzfunktion  , wenn die folgende Beziehung gilt:
, wenn die folgende Beziehung gilt:
Man schreibt





Next: Vertauschen von Grenzwerten
Up: Funktionsfolgen und Funktionsreihen
Previous: Funktionsfolgen und Funktionsreihen
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() konvergiert punktweise, wenn
konvergiert punktweise, wenn
![]() konvergiert. Die durch
konvergiert. Die durch
![]() in
in
![]() erklärte Funktion heißt Grenzfunktion.
erklärte Funktion heißt Grenzfunktion.
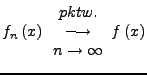
![]() ,
und
,
und
![]() seien beschränkt. Die
Folge
seien beschränkt. Die
Folge
![]() konvergiert gleichmäßig
gegen die Grenzfunktion
konvergiert gleichmäßig
gegen die Grenzfunktion ![]() , wenn die folgende Beziehung gilt:
, wenn die folgende Beziehung gilt: