




Next: wichtige Reihen II.154 /
Up: Funktionsfolgen und Funktionsreihen
Previous: Konvergenzkriterien
Contents
Index
Subsections
Potenzreihen II.185
Sei
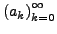 eine Folge und
eine Folge und
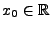 .
Die Reihe
.
Die Reihe
heißt Potenzreihe mit Koeffizienten
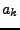 und Entwicklungspunkt
und Entwicklungspunkt 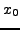 (z.B. Taylorreihe).
(z.B. Taylorreihe).
Konvergenz / Konvergenzradius
II.185
Sei
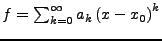 eine Potenzreihe,
die an der Stelle
eine Potenzreihe,
die an der Stelle 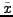 konvergiert. Dann konvergiert die Reihe
absolut und gleichmäßig
in jedem Intervall
konvergiert. Dann konvergiert die Reihe
absolut und gleichmäßig
in jedem Intervall
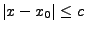 für jedes
für jedes
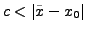 .
Divergiert
.
Divergiert  in
in 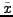 , so divergiert
, so divergiert  für alle
für alle 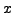 mit
mit
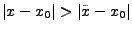 .
.
Wenn
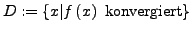 der Definitionsbereich von
der Definitionsbereich von  ist, heißt
ist, heißt
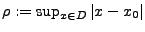 der Konvergenzradius von
der Konvergenzradius von  .
.
- In
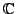 bildet
bildet 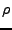 einen Kreis um
einen Kreis um 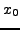
- über Punkte
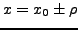 kann nichts ausgesagt werden
kann nichts ausgesagt werden
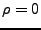 Konvergenz nur bei
Konvergenz nur bei 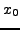
-
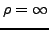 Konvergenz für alle
Konvergenz für alle 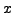
- eine Potenzreihe ist innerhalb ihres Konvergenzradius stets eine stetige
Funktion.
Konvergenzradius II.186
Sei
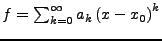 eine Potenzreihe.
Dann ist
eine Potenzreihe.
Dann ist
der Konvergenzradius. Die erste Formel ist die Hadamasche
Formel (gilt immer). Die Zweite Formel gilt nur, wenn dieser Grenzwert
auch existiert.
Sei
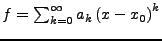 eine Potenzreihe
mit Konvergenzradius
eine Potenzreihe
mit Konvergenzradius 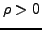 . Dann gilt
. Dann gilt
haben ebenfalls den Konvergenzradius 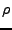 und
und
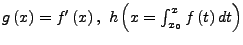 .
.
Wenn zwei Potenzreihen in einem beliebig kleinen Intervall
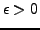 absolut konvergieren und übereinstimmen, sind sie bereits identisch
(
absolut konvergieren und übereinstimmen, sind sie bereits identisch
(
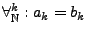 ).
).





Next: wichtige Reihen II.154 /
Up: Funktionsfolgen und Funktionsreihen
Previous: Konvergenzkriterien
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() eine Folge und
eine Folge und
![]() .
Die Reihe
.
Die Reihe
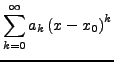
![]() eine Potenzreihe,
die an der Stelle
eine Potenzreihe,
die an der Stelle ![]() konvergiert. Dann konvergiert die Reihe
absolut und gleichmäßig
in jedem Intervall
konvergiert. Dann konvergiert die Reihe
absolut und gleichmäßig
in jedem Intervall
![]() für jedes
für jedes
![]() .
Divergiert
.
Divergiert ![]() in
in ![]() , so divergiert
, so divergiert ![]() für alle
für alle ![]() mit
mit
![]() .
.
![]() der Definitionsbereich von
der Definitionsbereich von ![]() ist, heißt
ist, heißt
![]() der Konvergenzradius von
der Konvergenzradius von ![]() .
.
![]() eine Potenzreihe.
Dann ist
eine Potenzreihe.
Dann ist
![$\displaystyle \rho=\frac{1}{\limsup_{k\rightarrow\infty}\sqrt[k]{\left\vert a_{...
...ight\vert}}=\lim_{k\rightarrow\infty}\left\vert\frac{a_{k}}{a_{k+1}}\right\vert$](img389.png)
![]() eine Potenzreihe
mit Konvergenzradius
eine Potenzreihe
mit Konvergenzradius ![]() . Dann gilt
. Dann gilt
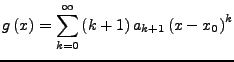
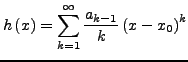
![]() absolut konvergieren und übereinstimmen, sind sie bereits identisch
(
absolut konvergieren und übereinstimmen, sind sie bereits identisch
(
![]() ).
).