Somit wäre
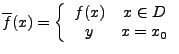 stetig.
stetig.
![]()
![]() hat den Grenzwert y, falls für jede gegen
hat den Grenzwert y, falls für jede gegen
![]() konvergente Folge,
konvergente Folge,
![]() ;
;
![]() ;
;
![]() folgendes gilt:
folgendes gilt:
![]()
![]() ist die stetige Fortsetzung von
ist die stetige Fortsetzung von ![]() in
in ![]() .
.
Somit wäre
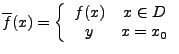 stetig.
stetig.
Die Funktion
![]() besitzt
in
besitzt
in ![]() den linksseitigen Grenzwert y, mit Zuhilfenahme einer
gegen
den linksseitigen Grenzwert y, mit Zuhilfenahme einer
gegen ![]() konvergenten Folge:
konvergenten Folge:
Die Funktion
![]() besitzt
in
besitzt
in ![]() den rechtsseitigen Grenzwert y, mit Zuhilfenahme einer
gegen
den rechtsseitigen Grenzwert y, mit Zuhilfenahme einer
gegen ![]() konvergenten Folge:
konvergenten Folge:
Eine Funktion besitzt in einem Punkt ![]() dann einen Grenzwert
dann einen Grenzwert
![]() , wenn ihr links-/rechtsseitiger Grenzwert übereinstimmen.
, wenn ihr links-/rechtsseitiger Grenzwert übereinstimmen.
Eine Funktion kann im Unendlichen einen Grenzwert besitzen. Z.B.
![]()
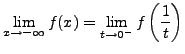
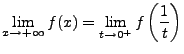
Eine Funktion besitzt eine Sprungstelle im Punkt ![]() , wenn:
, wenn:
Eine Funktion
![]() hat in
hat in ![]() eine hebbare Unstetigkeit, falls:
eine hebbare Unstetigkeit, falls:
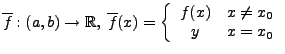 heißt stetige Fortsetzung von
heißt stetige Fortsetzung von
Wenn
![]() zu
zu
![]() oder
oder
![]() führt, dann lässt sich der Ausdurch
an der Stelle
führt, dann lässt sich der Ausdurch
an der Stelle ![]() durch die Ableitung von
durch die Ableitung von ![]() und
und ![]() ersetzen.
ersetzen.
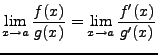
Um einen Ausdruck, der zu
![]() führt zu ersetzen, müssen
die Funktionen einfach angepasst werden. So wird aus
führt zu ersetzen, müssen
die Funktionen einfach angepasst werden. So wird aus
![]() .
Hier muss nur beachtet werden, dass hier
.
Hier muss nur beachtet werden, dass hier
![]() abgeleitet wird.
abgeleitet wird.
Wenn
![]() zu
zu
![]() führt, lässt sich dies häufig durch eine Taylorentwicklung
von Teilen von
führt, lässt sich dies häufig durch eine Taylorentwicklung
von Teilen von
![]() (z.B. Teile
des Nenners und des Zählers) umgehen. Dabei reicht es zumeist, die
ersten 3 bis 5 Glieder des Polynoms hinzuschreiben. Anschließend muss
versucht werden,
(z.B. Teile
des Nenners und des Zählers) umgehen. Dabei reicht es zumeist, die
ersten 3 bis 5 Glieder des Polynoms hinzuschreiben. Anschließend muss
versucht werden, ![]() so zu kürzen, das die Therme höherer Potenz
durch den Grenzübergang wegfallen, und nur noch ein (einfacher) Bruch
übrig bleibt.
so zu kürzen, das die Therme höherer Potenz
durch den Grenzübergang wegfallen, und nur noch ein (einfacher) Bruch
übrig bleibt.