




Next: Differenzierbare Funktionen II.64
Up: Funktionen I.116
Previous: Grenzwert von Funktionen
Contents
Index
Subsections
Logarithmus- und Exponentialfunktion
II.55
(eigentlich über Potenzreihen definiert)
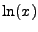 ist eine stetige, streng monoton wachsende Funktion auf
ist eine stetige, streng monoton wachsende Funktion auf
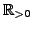 (II.57).
(II.57).
Umkehrfunkton von 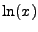 heißt
heißt
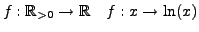
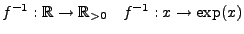
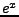 stetig und streng monoton wachsend auf
stetig und streng monoton wachsend auf
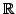 .
.
-
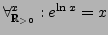
-
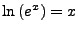
-
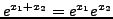
-
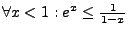
-
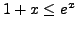
-
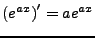
- Wachstumsverhalten der Exponentialfunktion
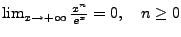
Allgemeine Exp. Funktion /
Logarithmus II.62
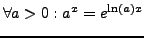 bzw.
bzw.
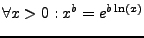
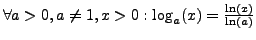
Marco Möller 17:42:11 24.10.2005
![$\displaystyle \ln x=\lim_{n\rightarrow\infty}2^{n}\left(\sqrt[2^{n}]{x}-1\right)=\lim_{n\rightarrow\infty}2^{n}\left(1-\frac{1}{\sqrt[2^{n}]{x}}\right)$](img496.png)
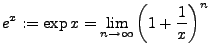
![]()
![]()
![]() stetig und streng monoton wachsend auf
stetig und streng monoton wachsend auf
![]() .
.
![]() bzw.
bzw.
![]()
![]()