Eine Funktion
![]() heißt differenzierbar im
inneren Punkt
heißt differenzierbar im
inneren Punkt
![]() , wenn der Grenzwert
, wenn der Grenzwert
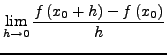 |
|||
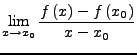 |
|||
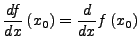 |
Ist ![]() ein Randpunkt des Intervalls
ein Randpunkt des Intervalls ![]() mit
mit
![]() ,
so heißt
,
so heißt ![]() in
in ![]() links-/ bzw. rechtsseitig differenzierbar,
wenn der links-/ bzw. rechtsseitige Grenzwert existiert.
links-/ bzw. rechtsseitig differenzierbar,
wenn der links-/ bzw. rechtsseitige Grenzwert existiert.
![]() gibt die Steigung einer Tangenten
von
gibt die Steigung einer Tangenten
von ![]() in
in ![]() wieder. Die Prozedur des Ableiten ist eine lineare
Abbildung
wieder. Die Prozedur des Ableiten ist eine lineare
Abbildung
![]() .
.
Eine Funktion
![]() ist genau dann differenzierbar
im Punkt
ist genau dann differenzierbar
im Punkt
![]() , wenn es ein
, wenn es ein
![]() und eine auf
einer
und eine auf
einer
![]() -Umgebung
-Umgebung
![]() erklärte
Funktion
erklärte
Funktion ![]() gibt, so daß
gibt, so daß
Die stetige Funktion
![]() sei
streng monoton und in
sei
streng monoton und in
![]() differenzierbar
mit
differenzierbar
mit
![]() . Dann ist die Umkehrfunktion
. Dann ist die Umkehrfunktion
![]() in
in ![]() differenzierbar, und es gilt
differenzierbar, und es gilt
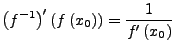
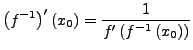
Ist ![]() stetig differenzierbar, dann ist auch
stetig differenzierbar, dann ist auch ![]() stetig differenzierbar.
stetig differenzierbar.
Alle Ableitungen nach ![]() (
(
![]() ).
).
Die Funktion ![]() besitzt an der Stelle
besitzt an der Stelle ![]() ein relatives Extremum,
dann gilt
ein relatives Extremum,
dann gilt
![]() . Dies ist aber nicht hinreichend
(nicht immer in umgekehrter Richtung gültig), da es sich auch um einen
Sattelpunkt handeln könnte.
. Dies ist aber nicht hinreichend
(nicht immer in umgekehrter Richtung gültig), da es sich auch um einen
Sattelpunkt handeln könnte.
Die Funktionen
![]() und
und
![]() seien stetig und in
seien stetig und in
![]() differenzierbar.
differenzierbar.
Sei
![]() stetig in
stetig in
![]() differenzierbar. Wenn für alle
differenzierbar. Wenn für alle
![]() :
: