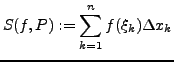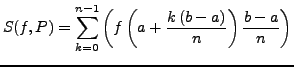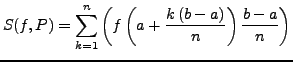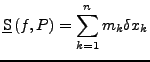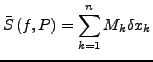Next: Riemann Integral II.100
Up: Integralrechnung II.92
Previous: Integralrechnung II.92
Contents
Index
Subsections
Ober- und Untersummen II.92
Zerlegung (Partition) II.92
Sei
![$ \left[a,b\right]$](img342.png) ein abgeschlossenes Intervall und
ein abgeschlossenes Intervall und
Dann bildet die Menge der 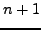 reellen Zahlen
reellen Zahlen
eine Partition von
![$ \left[a,b\right]$](img342.png) .
heißt Feinheit von
.
heißt Feinheit von 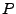 .
.
Eine äquidistante Zerlegung
ist wie folgt definiert
Riemann-Summe II.103
Sei
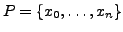 eine Zerlegung von
eine Zerlegung von
![$ \left[a,b\right]$](img342.png) und
und
Dann heißt
eine Riemann-Summe.
- linke Riemann-Summe
für
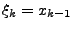
bei äuquidistanter Zerlegung
- rechte Riemann-Summe
für
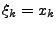
bei äuquidistanter Zerlegung
- untere Riemann-Summe
für
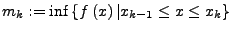
- obere Riemann-Summe
für
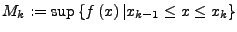
Marco Möller 17:42:11 24.10.2005
![]() ein abgeschlossenes Intervall und
ein abgeschlossenes Intervall und
![]() reellen Zahlen
reellen Zahlen
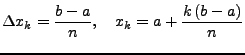
![]() eine Zerlegung von
eine Zerlegung von
![]() und
und