Riemann Integral II.100

Eine Funktion $f:\left[a,b\right]\rightarrow\mathbb{R}$ heißt Riemann-integrierbar auf $\left[a,b\right]$ wenn folgende Grenzwerte existieren und miteinander Übereinstimmen. Für diesen Grenzwert schreibt man

$$\int_{a}^{b}f\left(x\right)dx:=\lim_{\left\Vert P\right\Vert \rig... ...t(f,P\right)=\lim_{\left\Vert P\right\Vert \rightarrow0}\bar{S}\left(f,P\right)$$

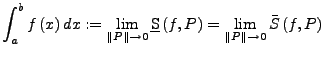
Im folgenden wird mit integrierbar immer Riemann-integrierbar gemeint (es gibt noch andere Integrierbarkeitsbegriffe).

Folgende Funktionen sind (Riemann) integrierbar

• monotone, beschränke Funktionen
• stetige Funktionen