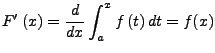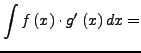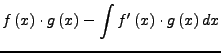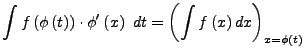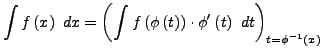Next: Uneigentliche Integrale II.131
Up: Integralrechnung II.92
Previous: Eigenschaften von Integralen II.99
Contents
Index
Subsections
Flächen- und Stammfunktion
/ unbestimmtes Integral II.103
Sei
![$ f:\left[a,b\right]\rightarrow\mathbb{R}$](img345.png) integrierbar
integrierbar
- Flächenfunktion
-
![$ F\left(x\right):=\int_{a}^{x}f\left(t\right)dt\;\left(x\in\left[a,b\right]\right)$](img630.png)
- unbestimmtes Integral
-
![$ F\left(x\right):=\int_{c}^{x}f\left(t\right)dt\;\left(x,c\in\left[a,b\right]\right)$](img631.png)
- Stammfunktion
-
![$ F'\left(x\right):=f\left(x\right)\;\left(x\in\left[a,b\right]\right)$](img632.png)
- Alle drei Begriffe sind bis auf Feinheiten gleichwertig.
- Es gibt mehrere verschiedene
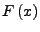 zu einer gegebenen
zu einer gegebenen
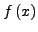 die sich nur durch eine Konstante unterscheiden
die sich nur durch eine Konstante unterscheiden
- Stammfunktionen sind in
![$ \left[a,b\right]$](img342.png) gleichmäßig stetig
gleichmäßig stetig
-
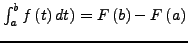
- Hauptsatz der Differential-
und Integralrechnung
- Integrieren ist Umkehroperation des Differenzieren
und umgekehrt
partielle Integration / Produktintegration
II.123
Partialbruchzerlegung
Durch Partialbruchzerlegung lassen sich rationale Funktionen
so schreiben, dass sie sich leichter integrieren lassen. Dabei kann
folgendes Schema angewandt werden.
- Polynomdivision, und die Funktion in der Form
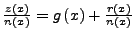 schreiben.
schreiben.
- Den Rest
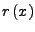 durch Partialbruchzerlegung vereinfachen,
dazu
durch Partialbruchzerlegung vereinfachen,
dazu
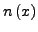 in Linearfaktoren
in Linearfaktoren
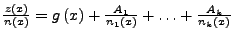 zerlegen. Jeder dieser Linearfaktoren wird zu einem Nenner eines Partialbruchs.
zerlegen. Jeder dieser Linearfaktoren wird zu einem Nenner eines Partialbruchs.
- Falls ein Linearfaktor
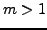 mal vorkommt, muss man ihn in mehrfach
als Nenner verwenden, und zwar so, das er als ganzen in den Potenzen
mal vorkommt, muss man ihn in mehrfach
als Nenner verwenden, und zwar so, das er als ganzen in den Potenzen
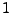 bis
bis 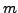 vorkommt.
vorkommt.
- Falls sich ein Nenner vom Rang
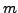 (im Reellen) nicht mehr weiter
Zerlegen lässt, ist es möglich ihn als ganzes beizubehalten. Dafür
muss im Zähler ein Polynom vom Grad
(im Reellen) nicht mehr weiter
Zerlegen lässt, ist es möglich ihn als ganzes beizubehalten. Dafür
muss im Zähler ein Polynom vom Grad 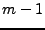 angenommen Werden, d.h.
angenommen Werden, d.h.
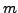 Unbekannte stehen vor den jeweiligen
Unbekannte stehen vor den jeweiligen 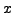 Potenzen auf dem Bruchstrich.
Potenzen auf dem Bruchstrich.
- Jedem Partialbruch eine Unbekannte
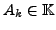 zuordnen.
zuordnen.
- Hauptnenner des Partialbruchs bilden und ausmultipizieren
- Nach gleichen Potenzen von
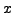 sortieren.
sortieren.
- Unbekannte durch Koeffizientenvergleich bestimmen.
- mit Hilfe lin. Gleichungssystem oder
- durch Einsetzen passender Werte für x, so das immer alles bis auf
eine Therm den Faktor 0 hat, und so wegfällt. So lässt sich dieser
Therm dann direkt auswerten.
- Kontrolle!!!
- Stammfunktion der Umgeformten Gleichung bestimmen. Fertig!!
Substitution
II.126
- Gebrauchsanweisung
- Eine passende Ersetzung suchen
-
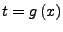
- diese Ableiten
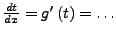
- umstellen
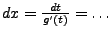
- Im Integral Substituieren mit Hilfe von (a).i (bzw.
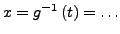 )
und (a).iii
)
und (a).iii
- Versuchen Stammfunktion zu bilden
- wenn es nicht klappt, evtl. andere Substitution versuchen
- evtl. passend klammern, um bekannte Integrale zu Nutzen
- Im Ergebnis (Stammfunktion) zurücksubstituieren mit (a).i
- Gebrauchsanweisung
- Eine passende Ersetzung suchen
-
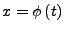
- diese Ableiten
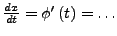
- umstellen
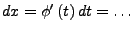
- Umkehrfunktion bilden
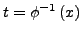
- Im Integral Subtituieren mit Hilfe von (a).i und (a).iii
- Versuchen Stammfunktion zu bilden
- wenn es nicht klappt, evtl. andere Substitution versuchen
- evtl. passend klammern, um bekannte Integrale zu Nutzen
- Im Ergebnis (Stammfunktion) zurücksubstituieren mit (a).i
- Beide Methoden äquivalent durch Regel der Ableitung der Umkehrfunktion.
- In der Tabelle cap:Substitution-unbestimmten-Int hat man eine
Übersicht von geeigneten Substitutionen.
- So Klammern und Substituieren, das es auf etwas bekanntes (z.B. Ableitungen
von Trigonometrischen-, Hyperbolischen- oder Areafunktioen) zurückführen
lässt.
- Auf jeden Fall Probe!!!





Next: Uneigentliche Integrale II.131
Up: Integralrechnung II.92
Previous: Eigenschaften von Integralen II.99
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() integrierbar
integrierbar