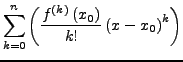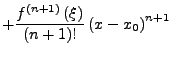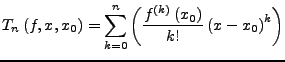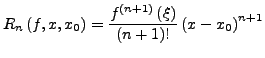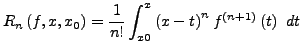Next: Taylorreihe II.152
Up: Taylorentwicklung II.141
Previous: Taylorentwicklung II.141
Contents
Index
Subsections
Satz von Taylor II.141
Die Funktion
![$ f:\left[a,b\right]\rightarrow\mathbb{R}$](img345.png) sei in
sei in
![$ \left[a,b\right]$](img342.png)
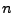 -mal stetig differenzierbar und im offenen Intervall
-mal stetig differenzierbar und im offenen Intervall
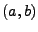
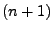 -mal differenzierbar. Sei
-mal differenzierbar. Sei
![$ x_{0}\in\left[a,b\right]$](img442.png) .
Dann gibt es zu jedem
.
Dann gibt es zu jedem
![$ x\in\left[a,b\right]$](img370.png) ein
ein 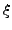 mit
mit
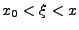 oder
oder
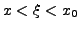 mit
mit
Taylorpolynom / Restglied
II.141
- Allgemein gilt
- Taylorpolynom der Funktion
 vom Grad
vom Grad 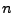 um den Entwicklungspunkt
um den Entwicklungspunkt
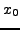 .
.
- Restglied in Lagrangeform
mit
![$ \xi\in\left[x_{0},x\right]\cup\left[x,x_{0}\right]$](img701.png)
- Restglied in Integralform
- wichtige Reihen siehe sub:Besondere-Reihen und sub:wichtige-Reihen-II.154.
Marco Möller 17:42:11 24.10.2005
![]() sei in
sei in
![]()
![]() -mal stetig differenzierbar und im offenen Intervall
-mal stetig differenzierbar und im offenen Intervall
![]()
![]() -mal differenzierbar. Sei
-mal differenzierbar. Sei
![]() .
Dann gibt es zu jedem
.
Dann gibt es zu jedem
![]() ein
ein ![]() mit
mit
![]() oder
oder
![]() mit
mit