




Next: Stetigkeit und Grenzwert II.203
Up: Funktionen mehrerer Veränderlicher II.199
Previous: Funktionen mehrerer Veränderlicher II.199
Contents
Index
Subsections
Euklidische Norm II.199
Sei
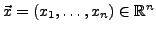 . Dann
heißt
. Dann
heißt
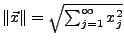 die euklidische Norm von
die euklidische Norm von 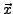 .
.
Konvergenz II.202
Eine Folge
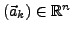 konvergiert
genau dann gegen den Grenzwert
konvergiert
genau dann gegen den Grenzwert
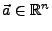 , wenn jede
Komponentenfolge
, wenn jede
Komponentenfolge
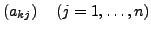 gegen
gegen 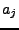 konvergiert.
konvergiert.
- Eine Folge ist genau dann konvergent, wenn sie eine Cauchyfolge
ist, d.h. wenn es zu jedem
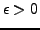 einen
einen
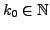 gibt mit
gibt mit
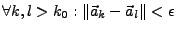
Randpunkt / Häufungspunkt
II.200
Ein
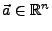 heißt Randpunkt von
heißt Randpunkt von
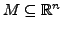 ,
wenn für jede
,
wenn für jede 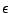 -Umgebung
-Umgebung
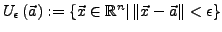 sowohl
sowohl
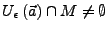 als
auch
als
auch
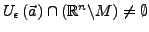 gilt.
gilt.
Ein 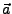 heißt Häufungspunkt von
heißt Häufungspunkt von 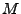 , falls es zu jeder
, falls es zu jeder
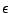 -Umgebung
-Umgebung
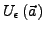 ein Element
ein Element
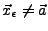 von
von 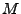 mit
mit
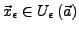 gibt.
gibt.
Ein
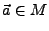 heißt innerer Punkt
heißt innerer Punkt
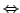
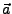 kein Randpunkt von
kein Randpunkt von 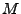 .
.
- Jede unendliche beschränkte Menge
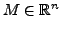 besitzt mindestens
einen Häufungspunkt (Satz von Bolzano-Weierstraß).
besitzt mindestens
einen Häufungspunkt (Satz von Bolzano-Weierstraß).
Abgeschlossen / Kompakt
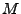 heißt abgeschlossen, wenn jeder Randpunkt von
heißt abgeschlossen, wenn jeder Randpunkt von 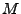 zu
zu
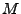 gehört.
gehört.
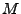 heißt kompakt, falls
heißt kompakt, falls 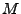 beschränkt und abgeschlossen
ist.
beschränkt und abgeschlossen
ist.





Next: Stetigkeit und Grenzwert II.203
Up: Funktionen mehrerer Veränderlicher II.199
Previous: Funktionen mehrerer Veränderlicher II.199
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() . Dann
heißt
. Dann
heißt
![]() die euklidische Norm von
die euklidische Norm von ![]() .
.
![]() konvergiert
genau dann gegen den Grenzwert
konvergiert
genau dann gegen den Grenzwert
![]() , wenn jede
Komponentenfolge
, wenn jede
Komponentenfolge
![]() gegen
gegen ![]() konvergiert.
konvergiert.
![]() heißt Randpunkt von
heißt Randpunkt von
![]() ,
wenn für jede
,
wenn für jede ![]() -Umgebung
-Umgebung
![]() sowohl
sowohl
![]() als
auch
als
auch
![]() gilt.
gilt.
![]() heißt Häufungspunkt von
heißt Häufungspunkt von ![]() , falls es zu jeder
, falls es zu jeder
![]() -Umgebung
-Umgebung
![]() ein Element
ein Element
![]() von
von ![]() mit
mit
![]() gibt.
gibt.
![]() heißt innerer Punkt
heißt innerer Punkt
![]()
![]() kein Randpunkt von
kein Randpunkt von ![]() .
.
![]() heißt abgeschlossen, wenn jeder Randpunkt von
heißt abgeschlossen, wenn jeder Randpunkt von ![]() zu
zu
![]() gehört.
gehört.
![]() heißt kompakt, falls
heißt kompakt, falls ![]() beschränkt und abgeschlossen
ist.
beschränkt und abgeschlossen
ist.