Eine Funktion
![]() , wobei
, wobei
![]() ,
heißt stetig in
,
heißt stetig in
![]() , wenn für jede Folge
, wenn für jede Folge
![]() ,
mit
,
mit
![]() gilt:
gilt:
![]() .
.
Sie heißt gleichmäßig stetig, falls
es zu jedem
![]() ein
ein ![]() gibt, so daß
gibt, so daß
Eine Funktion
![]() heißt stetig in
heißt stetig in
![]() , falls jede Komponente
, falls jede Komponente
![]() stetig ist.
stetig ist.
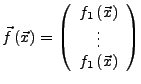
![]() ,
hat in
,
hat in
![]() den Grenzwert
den Grenzwert ![]() , falls für jede Folge
, falls für jede Folge
![]() mit
mit
![]() gilt:
gilt:
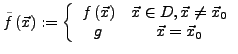
Eine Funktion
![]() hat in
hat in
![]() ein relatives Minimum (Maximum),
wenn es eine Umgebung
ein relatives Minimum (Maximum),
wenn es eine Umgebung
![]() gibt,
so daß
gibt,
so daß
![]() (
(
![]() )
für alle
)
für alle
![]() .
.
![]() heißt absolutes Minimum (Maximum),
wenn
heißt absolutes Minimum (Maximum),
wenn
![]() (
(
![]() )
für alle
)
für alle
![]() .
.