




Next: Differenzierbare Funktionen im II.219
Up: Funktionen mehrerer Veränderlicher II.199
Previous: Stetigkeit und Grenzwert II.203
Contents
Index
Subsections
Partielle Ableitung II.208
Sei
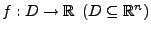 eine Funktion und
eine Funktion und
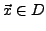 . Wenn der Grenzwert
. Wenn der Grenzwert
für ein
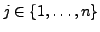 existiert, so heißt
existiert, so heißt  in
in 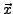 partiell nach
partiell nach 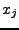 differenzierbar.
differenzierbar.
Gradient II.210
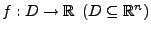 sei in
sei in
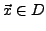 nach allen
nach allen
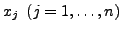 partiell differenzierbar. Dann heißt
partiell differenzierbar. Dann heißt
der Gradient von  im Punkt
im Punkt
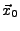 .
.
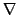 wird nabla gesprochen (ist kein echter griechischer Buchstabe)
wird nabla gesprochen (ist kein echter griechischer Buchstabe)
- Der Gradient gibt die Richtung des stärksten Anstiegs von
 in
in
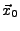 an
an
Richtungsableitung II.213
Sei
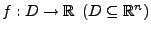 ,
,
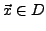 ,
,
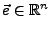 Einheitsvektor. Falls
Einheitsvektor. Falls
existiert, heißt  in
in 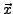 differenzierbar in Richtung
differenzierbar in Richtung
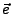 und
und
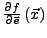 heißt Richtungsableitung von
heißt Richtungsableitung von  in Richtung
in Richtung 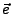 .
.
- Partielle Ableitung
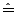 Richtungsableitung in Richtung der
Richtungsableitung in Richtung der
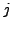 -ten Koordinate
-ten Koordinate
Die Funktion
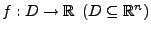 sei nach der Variablen
sei nach der Variablen 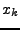 partiell differenzierbar. Im Punkt
partiell differenzierbar. Im Punkt
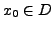 existiert die partielle Ableitung der Funktion
existiert die partielle Ableitung der Funktion
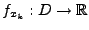 nach
nach 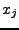 . Dann bezeichnet man
. Dann bezeichnet man
als partielle Ableitung zweiter Ordnung der Funktion  nach den
Variablen
nach den
Variablen 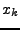 und
und 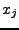 . Entsprechend werden partielle Ableitungen
höherer Ordnung erklärt.
. Entsprechend werden partielle Ableitungen
höherer Ordnung erklärt.
Hessematrix 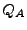 II.238
II.238
Die Hessematrix ist wie folgt definiert.
- ist symmetrisch, falls
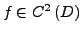 ist
ist
Differenzierbarkeitsklassen II.230
Sei
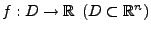 .
Wir schreiben
.
Wir schreiben
( gehört zu Klasse
gehört zu Klasse 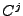 ) falls sämtliche partiellen Ableitungen
bis zur
) falls sämtliche partiellen Ableitungen
bis zur 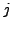 -ten Ordnung existieren und stetig sind.
-ten Ordnung existieren und stetig sind.
Satz von Schwarz / Vertauschbarkeit
der partiellen Ableitungen II.230
Sei
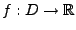 eine Funktion mit
eine Funktion mit
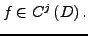 Dann gilt: Die mehrfache Ableitung
Dann gilt: Die mehrfache Ableitung
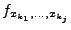 ist von der Reihenfolge der partiellen Ableitungen unabhängig, d.h.
für jede Permutation der Indizes ergibt sich das selbe Resultat.
ist von der Reihenfolge der partiellen Ableitungen unabhängig, d.h.
für jede Permutation der Indizes ergibt sich das selbe Resultat.
Parameterabhängige Integrale
II.216
Sei
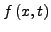 in
in
![$ D:=\left[a,b\right]\times\left[\alpha,\beta\right]$](img791.png) stetige, reellwertige Funktion mit stetiger partieller Ableitung
stetige, reellwertige Funktion mit stetiger partieller Ableitung
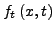 .
Dann ist für beliebige
.
Dann ist für beliebige
![$ x_{0}\in\left[a,b\right]$](img442.png) die Funktion
die Funktion
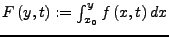 stetig und besitzt partielle Ableitungen
stetig und besitzt partielle Ableitungen
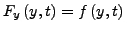 und
und
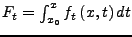 .
.
- eine art. Vertauschbarkeit von Grenzwerten





Next: Differenzierbare Funktionen im II.219
Up: Funktionen mehrerer Veränderlicher II.199
Previous: Stetigkeit und Grenzwert II.203
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() eine Funktion und
eine Funktion und
![]() . Wenn der Grenzwert
. Wenn der Grenzwert
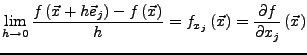
![]() sei in
sei in
![]() nach allen
nach allen
![]() partiell differenzierbar. Dann heißt
partiell differenzierbar. Dann heißt
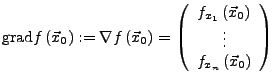
![]() ,
,
![]() ,
,
![]() Einheitsvektor. Falls
Einheitsvektor. Falls
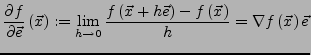
![]() sei nach der Variablen
sei nach der Variablen ![]() partiell differenzierbar. Im Punkt
partiell differenzierbar. Im Punkt
![]() existiert die partielle Ableitung der Funktion
existiert die partielle Ableitung der Funktion
![]() nach
nach ![]() . Dann bezeichnet man
. Dann bezeichnet man
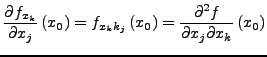
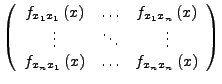
![]() .
Wir schreiben
.
Wir schreiben
![]() eine Funktion mit
eine Funktion mit
![]() Dann gilt: Die mehrfache Ableitung
Dann gilt: Die mehrfache Ableitung
![]() ist von der Reihenfolge der partiellen Ableitungen unabhängig, d.h.
für jede Permutation der Indizes ergibt sich das selbe Resultat.
ist von der Reihenfolge der partiellen Ableitungen unabhängig, d.h.
für jede Permutation der Indizes ergibt sich das selbe Resultat.
![]() in
in
![]() stetige, reellwertige Funktion mit stetiger partieller Ableitung
stetige, reellwertige Funktion mit stetiger partieller Ableitung
![]() .
Dann ist für beliebige
.
Dann ist für beliebige
![]() die Funktion
die Funktion
![]() stetig und besitzt partielle Ableitungen
stetig und besitzt partielle Ableitungen
![]() und
und
![]() .
.