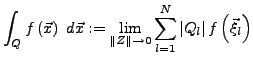Next: Integrierte Integrale über Intervallen
Up: Integration im II.256
Previous: Integration im II.256
Contents
Index
Subsections
Riemann-Integrale über Intervallen
Zerlegung / Feinheit
Der Grundbereich über dem die Integration stattfinden soll heiße
![$ Q=\left[a_{1},b_{1}\right]\times\ldots\times\left[a_{n},b_{n}\right]$](img878.png) .
Dieser hat die Zerlegung
.
Dieser hat die Zerlegung 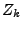 der Intervalle
der Intervalle
![$ \left[a_{k},b_{k}\right]$](img880.png) ,
,
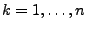 . Die Feinheit der Zerlegung
ist gegeben durch
. Die Feinheit der Zerlegung
ist gegeben durch
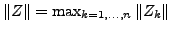 .
Zur Zerlegung
.
Zur Zerlegung 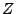 von
von 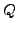 bezeichnen wir mit
bezeichnen wir mit
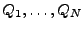 die Teile von
die Teile von 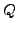 , also
, also
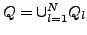
Für
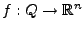 , definiere Integral
, definiere Integral
mit
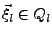 (
(
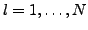 ). Wobei
). Wobei
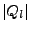 =
``Volumen'' von
=
``Volumen'' von 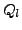 bezeichnet, also bei
bezeichnet, also bei
![$ Q_{l}=\left[c_{1},d_{1}\right]\times\ldots\times\left[c_{n},d_{n}\right]\Rightarrow\left\vert Q_{l}\right\vert=\prod_{l=1}^{n}\left\vert d_{1}-c_{1}\right\vert$](img893.png) .
Falls der Grenzwert existiert, so heißt
.
Falls der Grenzwert existiert, so heißt  Riemann-integrierbar.
Riemann-integrierbar.





Next: Integrierte Integrale über Intervallen
Up: Integration im II.256
Previous: Integration im II.256
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() .
Dieser hat die Zerlegung
.
Dieser hat die Zerlegung ![]() der Intervalle
der Intervalle
![]() ,
,
![]() . Die Feinheit der Zerlegung
ist gegeben durch
. Die Feinheit der Zerlegung
ist gegeben durch
![]() .
Zur Zerlegung
.
Zur Zerlegung ![]() von
von ![]() bezeichnen wir mit
bezeichnen wir mit
![]() die Teile von
die Teile von ![]() , also
, also
![]()
![]() , definiere Integral
, definiere Integral