




Next: Riemann Integrale über beschränkte
Up: Integration im II.256
Previous: Riemann-Integrale über Intervallen
Contents
Index
Subsections
Satz von Fubini II.263
Sei
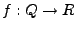 ,
,
![$ Q:=\left[a_{1},b_{1}\right]\times\ldots\times\left[a_{n},b_{n}\right]=\times_{k=1}^{n}\left[a_{k},b_{k}\right]$](img912.png) ein Quader.
ein Quader.
Existiert für jedes 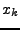
wobei
dann existiert das Integral
und es gilt
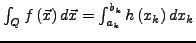 bzw.
bzw.
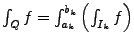 .
.
Existiert für jedes
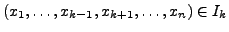 das Integral
das Integral
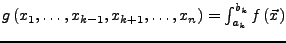 dann existiert das integrierte Integral
dann existiert das integrierte Integral
und ist gleich
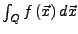 . Es gilt
auch
. Es gilt
auch
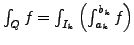
- speziell für
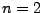
![$ Q=\left[a,b\right]\times\left[c,d\right]$](img924.png)
Existiert für
![$ x\in\left[a,b\right]$](img370.png) das Integral
das Integral
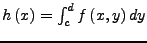
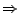
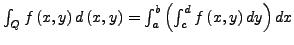
Existiert für
![$ y\in\left[c,d\right]$](img927.png) das Integral
das Integral
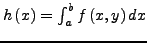
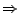
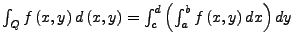
Charakteristische Funktion
Sei
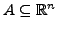 . Mit
. Mit
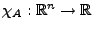
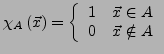 bezeichnen wir die charakteristische Funktion von
bezeichnen wir die charakteristische Funktion von  .
.
Marco Möller 17:42:11 24.10.2005
![]()
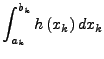
![]() das Integral
das Integral
![]() dann existiert das integrierte Integral
dann existiert das integrierte Integral
![]() . Mit
. Mit
![]()
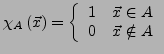 bezeichnen wir die charakteristische Funktion von
bezeichnen wir die charakteristische Funktion von ![]() .
.