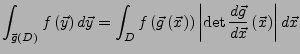Sei
![]() eine beschränkte Menge. Es existiere
eine beschränkte Menge. Es existiere
![]() . Dann heißt
. Dann heißt
![]() das Volumen der Menge
das Volumen der Menge ![]() . In diesem Fall heißt
. In diesem Fall heißt ![]() messbar.
Ist
messbar.
Ist
![]() , so heißt D eine Nullmenge.
, so heißt D eine Nullmenge.
Sei
![]() ein Quader,
ein Quader,
![]() .
Kennt man das
.
Kennt man das ![]() dimensionale Volumen
dimensionale Volumen
![]() für
jedes
für
jedes ![]() , so gilt
, so gilt
![]() (Prinzip von Cavalieri).
(Prinzip von Cavalieri).
Sei
![]() beschränkt,
beschränkt,
![]() Funktion. Sei
Funktion. Sei ![]() ein Quader mit
ein Quader mit
![]() . Dann heißt
. Dann heißt
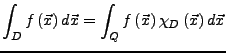
Sei
![]() beschränkt, messbar,
beschränkt, messbar, ![]() integrierbar.
Dann gibt es eine Zahl
integrierbar.
Dann gibt es eine Zahl
![]() mit
mit
![]() .
.
Folgendes sind Zylindermengen.
Sei
![]() dann folgt hieraus
dann folgt hieraus
![]() .
.
Sei
![]() dann folgt hieraus
dann folgt hieraus
![]() .
.
Sei
![]() beschränkt und messbar. Sei
beschränkt und messbar. Sei ![]() ein
Quader mit
ein
Quader mit
![]() und
und
![]() eine stetig differenzierbare Funktion, die auf
eine stetig differenzierbare Funktion, die auf ![]() umkehrbar ist.
umkehrbar ist.
Gilt dann
![]() für alle
für alle
![]() , so gilt für jedes stetige
, so gilt für jedes stetige
![]() die Substitutionsregel:
die Substitutionsregel: