(geometrisch: Betrag von
Das skalare Produkt ordnet zwei Vektoren eine reelle Zahl zu.
(geometrisch: Betrag von ![]() in Richtung
in Richtung ![]() )
)
Zwei Vektoren ![]() und
und ![]() schließen den Winkel
schließen den Winkel ![]() ein.
ein.
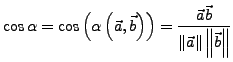
Ein Einheitsvektor (![]() ) ist ein Vektor mit beliebiger Richtung
und der Länge 1. Man erhält ihn durch Renormierung.
) ist ein Vektor mit beliebiger Richtung
und der Länge 1. Man erhält ihn durch Renormierung.
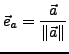
![]() ist die Projektion des Vektors
ist die Projektion des Vektors ![]() in Richtung
in Richtung
![]() (
(
![]() ).
).
Die Komponenten eines renormierten Vektors ![]() geben den Cosinus
der Winkel mit den Einheitsvektoren der Koordinatenachsen an.
geben den Cosinus
der Winkel mit den Einheitsvektoren der Koordinatenachsen an.