




Next: Vektorräume I.159
Up: Vektorrechnung in I.76
Previous: Spatprodukt I.95
Contents
Index
Subsections
Gerade und Ebene im Raum I.99
Geradengleichung I.99
Ebenengleichung I.107
Lage von Geraden im Raum I.99
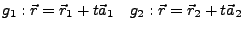
-
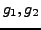 parallel zueinander
parallel zueinander
-
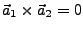
- Sonderfall
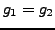 wenn zusätzlich
wenn zusätzlich
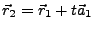
-
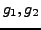 schneiden sich in genau einem Punkt
schneiden sich in genau einem Punkt
-
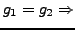 Schnittpunkt
Schnittpunkt
-
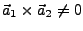
-
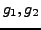 windschief zueinander (weder parallel noch Schnittpunkt)
windschief zueinander (weder parallel noch Schnittpunkt)
Abstand Gerade Punkt I.105
Gerade:
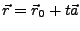 , Punkt:
, Punkt:
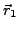 , Abstand
, Abstand
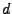
Abstand zweier windschiefer Geraden I.106
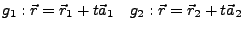
Normalenvektor I.108
Jeder auf der Ebene
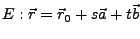 senkrecht
stehende Vektor
senkrecht
stehende Vektor 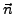 wird als Normalenvektor der Ebene
wird als Normalenvektor der Ebene 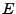 bezeichnet.
bezeichnet.
Lage zweier Ebenen im Raum I.111
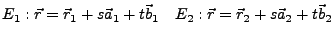
-
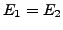 (sind gleich)
(sind gleich)
-
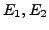 sind parallel aber nicht gleich
sind parallel aber nicht gleich
-
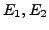 schneiden sich in einer Geraden
schneiden sich in einer Geraden
-
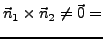 Richtungsvektor der Schnittgeraden
Richtungsvektor der Schnittgeraden
- Ortsvektor der Schnittgeraden ist ein beliebiger Punkt der auf
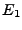 und
und 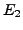 liegt.
liegt.
Schnittpunkt Gerade Ebene I.110
Der Schnittpunkt der Ebene
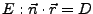 und der Gerade
und der Gerade
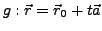 hat den Ortsvektor
hat den Ortsvektor
Lot auf Ebene I.111
Die Lotgerade auf der Ebene
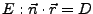 durch den Punkt
durch den Punkt 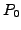 mit dem Ortsvektor
mit dem Ortsvektor
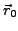 besitzt
folgende Gestalt
besitzt
folgende Gestalt
Der Ortsvektor des Fußpunktes (Durchstoßpunkt mit der Ebene) ergibt
sich dann so
Der Abstand einer Ebene
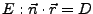 vom Ursprung
vom Ursprung
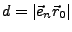
Der Abstand einer Ebene
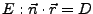 vom Punkt
vom Punkt
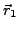
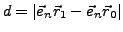





Next: Vektorräume I.159
Up: Vektorrechnung in I.76
Previous: Spatprodukt I.95
Contents
Index
Marco Möller 17:42:11 24.10.2005
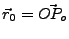
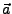
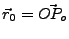
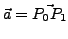
![]()
![]() , Punkt:
, Punkt:
![]() , Abstand
, Abstand
![]()
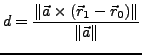
![]()
![$\displaystyle d=\frac{\left\vert\left[\vec{a}_{1},\vec{a}_{2},\vec{r}_{2}-\vec{r}_{1}\right]\right\vert}{\left\Vert \vec{a}_{1}\times\vec{a}_{2}\right\Vert }$](img1097.png)
![]() senkrecht
stehende Vektor
senkrecht
stehende Vektor ![]() wird als Normalenvektor der Ebene
wird als Normalenvektor der Ebene ![]() bezeichnet.
bezeichnet.
![]()
![]() und der Gerade
und der Gerade
![]() hat den Ortsvektor
hat den Ortsvektor
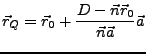
![]() durch den Punkt
durch den Punkt ![]() mit dem Ortsvektor
mit dem Ortsvektor
![]() besitzt
folgende Gestalt
besitzt
folgende Gestalt
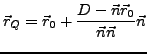
![]() vom Ursprung
vom Ursprung
![]()
![]() vom Punkt
vom Punkt
![]()
![]()