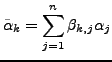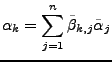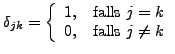Next: Der unitäre Vektorraum I.177
Up: Vektorräume I.159
Previous: Endlich-dimensionale Vektorräume I.166
Contents
Index
Subsections
Koordinaten I.171
Ein Vektor 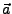 lässt sich mit Hilfe der Koordinaten
lässt sich mit Hilfe der Koordinaten
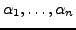 bezüglich der Basis
bezüglich der Basis
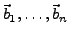 wie folgt (eindeutig)
darstellen.
wie folgt (eindeutig)
darstellen.
- Bezüglich der Kanonischen Basis sind die Koordinaten genau die Komponenten
des Vektors
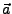
- Der Vektor der Koordinaten heißt Koordinatenvektor
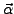
- Die Rechenregeln für Summe von zwei Koordinatenvektoren der gleichen
Basis und die Regeln der Multiplikation mit einem Skalar sind identisch
mit den Regeln für Vektoren.
-
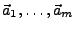 linear unabhängig
linear unabhängig
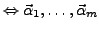 linear unabhängig
linear unabhängig
Basiswechsel
I.174
Seien
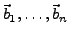 und
und
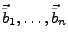 zwei Basen des n-dimensionalen Vektorraumes
zwei Basen des n-dimensionalen Vektorraumes
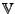 . Die Basisvektoren
haben nun sollen folgende Beziehungen untereinander besitzen
. Die Basisvektoren
haben nun sollen folgende Beziehungen untereinander besitzen
Die Koordinatenvektoren
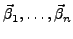 und
und
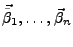 sind linear
unabhängig.
sind linear
unabhängig.
Einen Vektor 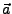 kann man nun in beiden Basissystemen ausdrücken
kann man nun in beiden Basissystemen ausdrücken
Zwischen den Koordinatenvektoren
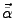 und
und
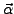 in den jeweiligen Basissystemen besteht der Zusammenhang:
in den jeweiligen Basissystemen besteht der Zusammenhang:
- Für weiteres siehe sub:BasiswechselMatix
Kronecker-Symbol I.176
Das Kronecker-Symbol ist wie folgt definiert





Next: Der unitäre Vektorraum I.177
Up: Vektorräume I.159
Previous: Endlich-dimensionale Vektorräume I.166
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() lässt sich mit Hilfe der Koordinaten
lässt sich mit Hilfe der Koordinaten
![]() bezüglich der Basis
bezüglich der Basis
![]() wie folgt (eindeutig)
darstellen.
wie folgt (eindeutig)
darstellen.
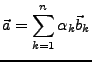
![]() und
und
![]() zwei Basen des n-dimensionalen Vektorraumes
zwei Basen des n-dimensionalen Vektorraumes
![]() . Die Basisvektoren
haben nun sollen folgende Beziehungen untereinander besitzen
. Die Basisvektoren
haben nun sollen folgende Beziehungen untereinander besitzen
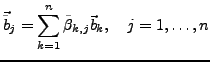
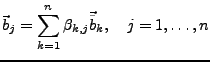
![]() kann man nun in beiden Basissystemen ausdrücken
kann man nun in beiden Basissystemen ausdrücken
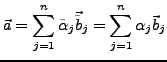
![]() und
und
![]() in den jeweiligen Basissystemen besteht der Zusammenhang:
in den jeweiligen Basissystemen besteht der Zusammenhang: