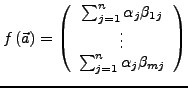Next: Matrizen I.190
Up: Vektorräume I.159
Previous: Der unitäre Vektorraum I.177
Contents
Index
Subsections
Lineare Abbildungen I.183
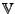 (Quellraum) und
(Quellraum) und
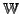 (Zielraum)
seien Vektorräume über demselben skalaren Körper
(Zielraum)
seien Vektorräume über demselben skalaren Körper
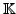 . Die
Abbildung
. Die
Abbildung
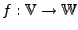 heißt linear,
wenn für alle
heißt linear,
wenn für alle
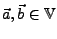 und
und
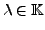 gilt:
gilt:
- Additivität
-
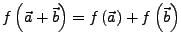
- Homogenität
-
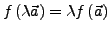
Eine Lineare Abbildung zwischen zwei Vektorräumen wird auch als Homomorphismus
bezeichnet.
-
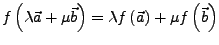
-
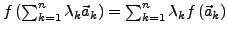
- integrieren und differenzieren von Polynomen sind lineare Abbildungen
Bild und Kern I.184
Sei
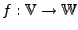 lineare Abbildung.
lineare Abbildung.
- Bild
- Bild
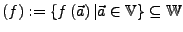
- Kern
- Kern
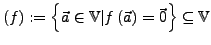
- Bild
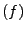 ist Untervektorraum von
ist Untervektorraum von
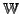
- Kern
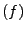 ist Untervektorraum von
ist Untervektorraum von
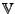
-
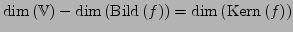
-
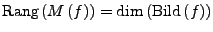
Injektiv / Surjektiv I.184
Eine Abbildung
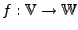 heißt injektiv,
falls
heißt injektiv,
falls
Bei linearen  gilt weiter:
gilt weiter:
 ist injektiv
ist injektiv
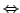 Kern
Kern
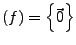
 ist surjektiv
ist surjektiv
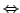
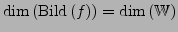
Um eine lineare Abbildung  festzulegen genügt es die Bilder
festzulegen genügt es die Bilder
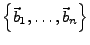 der Basis
der Basis
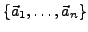 zu kennen,
für
zu kennen,
für
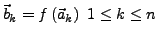 .
.
Sei
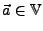 und
und
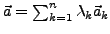 für geeignete
für geeignete
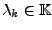 gilt
gilt
Koordinatenschreibweise linearer
Abbildungen I.188
Seien
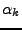
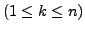 die Koordinaten
von
die Koordinaten
von 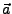 bezüglich der Basis
bezüglich der Basis
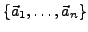 von
von
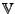 . Außerdem beschreibt
. Außerdem beschreibt
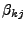 die Umrechnungskoordinaten
von
die Umrechnungskoordinaten
von
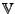 nach
nach
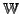
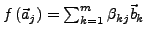 (
(
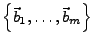 ist Basis von
ist Basis von
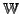 ). Dann gilt:
). Dann gilt:





Next: Matrizen I.190
Up: Vektorräume I.159
Previous: Der unitäre Vektorraum I.177
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() (Quellraum) und
(Quellraum) und
![]() (Zielraum)
seien Vektorräume über demselben skalaren Körper
(Zielraum)
seien Vektorräume über demselben skalaren Körper
![]() . Die
Abbildung
. Die
Abbildung
![]() heißt linear,
wenn für alle
heißt linear,
wenn für alle
![]() und
und
![]() gilt:
gilt:
![]() lineare Abbildung.
lineare Abbildung.
![]() heißt injektiv,
falls
heißt injektiv,
falls
![]() gilt weiter:
gilt weiter:
![]() festzulegen genügt es die Bilder
festzulegen genügt es die Bilder
![]() der Basis
der Basis
![]() zu kennen,
für
zu kennen,
für
![]() .
.
![]() und
und
![]() für geeignete
für geeignete
![]() gilt
gilt
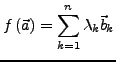
![]()
![]() die Koordinaten
von
die Koordinaten
von ![]() bezüglich der Basis
bezüglich der Basis
![]() von
von
![]() . Außerdem beschreibt
. Außerdem beschreibt
![]() die Umrechnungskoordinaten
von
die Umrechnungskoordinaten
von
![]() nach
nach
![]()
![]() (
(
![]() ist Basis von
ist Basis von
![]() ). Dann gilt:
). Dann gilt: