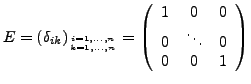Next: Rang einer Matrix I.200
Up: Matrizen I.190
Previous: Matrizen I.190
Contents
Index
Subsections
Die Addition erfolgt Elementenweise
(mit
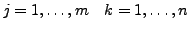 ):
):
Skalarmultiplikation I.195
Jedes Element wird einzeln Multipliziert
(mit
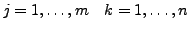 ):
):
Kanonische Basis
Die Kanonische Basis zu einem Vektorraum aller 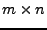 -Matrizen
besteht aus allen (verschiedenen)
-Matrizen
besteht aus allen (verschiedenen) 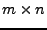 -Matrizen die jeweils
nur eine
-Matrizen die jeweils
nur eine 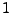 und sonst nur 0-en enthalten. Es gibt
und sonst nur 0-en enthalten. Es gibt 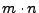 solcher Basen.
solcher Basen.
Transponierte Matrix I.192
Die 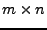 -Matrix
-Matrix  ist wie folgt definiert
ist wie folgt definiert
dann heißt die 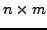 -Matrix
-Matrix
die zu  transponierte Matrix.
transponierte Matrix.
Alle (Anti-)Symmetrische Matrizen sind quadratische
Matrizen. Das bedeutet, das sie die gleiche
Anzahl an Spalten und Zeilen haben (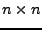 -Matrix).
-Matrix).
- symmetrische Matrix
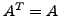
- Lässt sich auf der Hauptdiagonalen spiegeln, ohne das sie sich ändert
- antisymmetrische Matrix
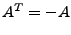
- Hat auf der Hauptdiagonalen nur 0en.
- Ist auf der Hauptdiagonalen mit vertauschten Vorzeichen gespiegelt.
- symmetrischer Teil
-
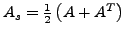
- antisymmetrischer Teil
-
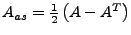
Matrixprodukt I.197
Sei
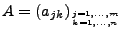 eine
eine 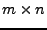 -Matrix und
-Matrix und
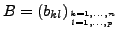 eine
eine 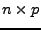 -Matrix. Die
-Matrix. Die 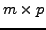 -Matrix
-Matrix
heißt Produktmatrix (Produkt aus  und
und 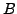 ).
).
- An Position
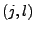 steht das Skalarprodukt des
steht das Skalarprodukt des 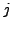 -ten
Zeilenvektors (der linken Matrix), mit dem
-ten
Zeilenvektors (der linken Matrix), mit dem 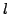 -ten Spaltenvektor
(der 2ten Matrix)
-ten Spaltenvektor
(der 2ten Matrix)
- Skalarprodukt von 2 Vektoren ist Sonderfall des Matrixproduktes
- Produkt entspricht der Hintereinanderausführung von linearen Abbildungen
- Nur Definiert, wenn Spaltenanzahl der 1. Matrix = Zeilenanzahl der
2. Matrix
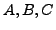 seien Matrizen, so dass die folgenden Produkte definiert
sind
seien Matrizen, so dass die folgenden Produkte definiert
sind
- Assoziativgesetz
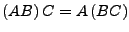
- Distributivgesetz
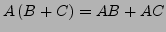
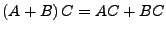
-
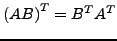
- im allgemeinen:
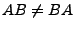
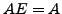 (mit
(mit 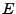 = Einheitsmatrix)
= Einheitsmatrix)
- nilpotent heißt eine Matrix, wenn
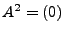 = Nullmatrix
= Nullmatrix
- Die Menge aller
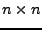 -Matrizen mit den Rechengesetzen zusammen
bildet einen Ring. Keinen Körper, da das inverse
Element der Muliplikation im allgemeinen nicht Existiert.
-Matrizen mit den Rechengesetzen zusammen
bildet einen Ring. Keinen Körper, da das inverse
Element der Muliplikation im allgemeinen nicht Existiert.
Nullmatrix
Eine Matrix die ausschließlich mit Nullen aufgefüllt ist, nennt sich
Nullmatrix, und hat den Rang 0.
Einheitsmatrix I.200
Eine 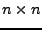 -Matrix die
-Matrix die 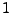 en auf der Hauptdiagonale, und sonst
nur Nullen hat, heißt Einheitsmatix. Sie ist das neutrales
Element der Multiplikation.
en auf der Hauptdiagonale, und sonst
nur Nullen hat, heißt Einheitsmatix. Sie ist das neutrales
Element der Multiplikation.





Next: Rang einer Matrix I.200
Up: Matrizen I.190
Previous: Matrizen I.190
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() ):
):
![]() ):
):
![]() -Matrizen
besteht aus allen (verschiedenen)
-Matrizen
besteht aus allen (verschiedenen) ![]() -Matrizen die jeweils
nur eine
-Matrizen die jeweils
nur eine ![]() und sonst nur 0-en enthalten. Es gibt
und sonst nur 0-en enthalten. Es gibt ![]() solcher Basen.
solcher Basen.
![]() -Matrix
-Matrix ![]() ist wie folgt definiert
ist wie folgt definiert
![]() transponierte Matrix.
transponierte Matrix.
![]() -Matrix).
-Matrix).
![]() eine
eine ![]() -Matrix und
-Matrix und
![]() eine
eine ![]() -Matrix. Die
-Matrix. Die ![]() -Matrix
-Matrix 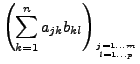
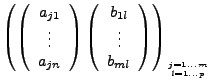
![]() -Matrix die
-Matrix die ![]() en auf der Hauptdiagonale, und sonst
nur Nullen hat, heißt Einheitsmatix. Sie ist das neutrales
Element der Multiplikation.
en auf der Hauptdiagonale, und sonst
nur Nullen hat, heißt Einheitsmatix. Sie ist das neutrales
Element der Multiplikation.