Lineare Abbildungen und Matrizen I.213

Next: Lineare Gleichungssysteme I.220 Up: Matrizen I.190 Previous: Rang einer Matrix I.200 Contents Index

Subsections

Lineare Abbildungen und Matrizen I.213

Menge aller linearen Abbildungen I.214

Sei $L\left(\mathbb{V},\mathbb{W}\right)$ die Menge aller lin. Abbildungen von $\mathbb{V}$ nach $\mathbb{W}$ .

$\dim\mathbb{V}=n\wedge\dim\mathbb{W}=m\Rightarrow\dim L\left(\mathbb{V},\mathbb{W}\right)=nm$

Zuordnung Matrix $\Leftrightarrow$ Lin. Abbildung I.214

Sei $\vec{a}_{1},\ldots,\vec{a}_{n}$ eine Basis von $\mathbb{V}$ und $\vec{b}_{1},\ldots,\vec{b_{m}}$ eine Basis von $\mathbb{W}$ . Für jede lin. Abbildung $f\in L\left(\mathbb{V},\mathbb{W}\right)$ lässt sich nun eine $m\times n$ Matrix zuordnen. Sei

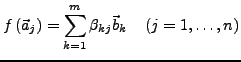
$\displaystyle f\left(\vec{a}_{j}\right)=\sum_{k=1}^{m}\beta_{kj}\vec{b}_{k}\quad\left(j=1,\ldots,n\right)$

dann hat die Matrix folgende Gestalt

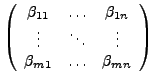$\displaystyle M\left(f\right)$	$\displaystyle =$	$\displaystyle \left(\begin{array}{ccc} \beta_{11} & \ldots & \beta_{1n}\\ \vdots & \ddots & \vdots\\ \beta_{m1} & \ldots & \beta_{mn}\end{array}\right)$
	$\displaystyle =$	$\displaystyle \left(\begin{array}{ccc} f\left(\vec{a}_{1}\right) & \ldots & f\left(\vec{a}_{n}\right)\end{array}\right)$
	$\displaystyle =$	$\displaystyle \left(\beta_{kj}\right)_{{{k=1,\ldots,m\atop j=1,\ldots,n}}}$

Sei $\vec{x}\in\mathbb{V}$ ein Koordinatenvektor bezüglich der oben gewählten Basis.

$\displaystyle M\left(f\right)\vec{x}=f\left(\vec{x}\right)$

Achtung, Reihenfolge der Muliplikation entscheidend!
$\textrm{Rang}\left(M\left(f\right)\right)=\dim\left(\textrm{Bild}\left(f\right)\right)$

Verkettung von lin. Abbildungen I.216

Die Matrix der Hintereinanderausführung zweier lin. Abbildungen $f\in L\left(\mathbb{V},\mathbb{W}\right)$ und $g\in L\left(\mathbb{W},\mathbb{U}\right)$ ist $M\left(g\circ f\right)=M\left(g\right)M\left(f\right)=M\left(g\left(f\right)\right)$

Inverse Matrix I.216

Sei $f:\mathbb{V}\rightarrow\mathbb{V}$ linear, $\dim\mathbb{V}=n$ mit $\dim\textrm{Bild}\left(f\right)=n=\dim\mathbb{V}$ ( ist injektiv). Dann muss eine Umkehrabbildung $f^{-1}:\mathbb{V}\rightarrow\mathbb{V}$ mit $f^{-1}\circ f=\textrm{id}_{\mathbb{V}}=f\circ f^{-1}$ existieren.

Sei $A=M\left(f\right),A^{-1}=M\left(f^{-1}\right)$ dann folgt $AA^{-1}=M\left(id_{\mathbb{V}}\right)=E=A^{-1}A$ . $A^{-1}$ heißt die zu inverse Matrix.