




Next: Kontextfreie Sprachen (Typ 2)
Up: Reguläre Sprachen (Typ 3)
Previous: Abschlusseigenschaften 48
Contents
Index
Subsections
Entscheidbarkeit 49
Wortproblem
Das Wortproblem (gegeben: 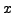 , gefragt: ist
, gefragt: ist
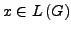 bzw.
bzw.
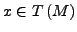 ) ist mit Hilfe eines DFA leicht möglich.
Verfolge einfach Zeichen für Zeichen die Zustandsübergänge im Automaten,
die durch die Eingabe
) ist mit Hilfe eines DFA leicht möglich.
Verfolge einfach Zeichen für Zeichen die Zustandsübergänge im Automaten,
die durch die Eingabe 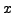 hervorgerufen werden. Falls ein Endzustand
erreicht wird, liegt
hervorgerufen werden. Falls ein Endzustand
erreicht wird, liegt 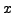 in der Sprache. Die Laufzeitkomplexität
beträgt hier
in der Sprache. Die Laufzeitkomplexität
beträgt hier
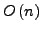 .
.
Leerheitsproblem
Das Leerheitsproblem stellt bei gegebenem 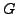 (bzw.
(bzw. 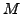 )
die Frage, ob
)
die Frage, ob
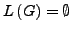 (bzw.
(bzw.
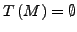 ).
Sei
).
Sei 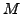 ein gegebener Automat für die Sprache.
ein gegebener Automat für die Sprache.
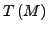 ist genau dann leer, wenn es keinen Pfad vom (einem) Startzustand
zu einem Endzustand gibt.
ist genau dann leer, wenn es keinen Pfad vom (einem) Startzustand
zu einem Endzustand gibt.
Endlichkeitsproblem
Das Endlichkeitsproblem stellt bei gegebenem 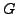 (bzw.
(bzw. 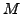 )
die Frage, ob
)
die Frage, ob
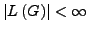 (bzw.
(bzw.
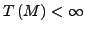 ),
also ob die definierte Sprache endlich oder unendlich ist.
),
also ob die definierte Sprache endlich oder unendlich ist.
Hier gibt es zwei Verfahren:
- Sei
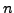 die Pumping Lemma (siehe sub:Das-Pumping-Lemma) Zahl
zu
die Pumping Lemma (siehe sub:Das-Pumping-Lemma) Zahl
zu 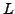 . Es gilt:
. Es gilt:
- Diese Argument verläuft so, dass alle Wörter der Länge
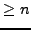 und
und
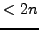 auf Mitgliedschaft in
auf Mitgliedschaft in 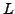 geprüft werden müssen.
geprüft werden müssen.
- Die Laufzeitkomplexität beträgt
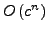
- Es ist
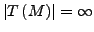 genau dann, wenn es
in dem von Startzustand erreichbaren Teilgraphen einen Zyklus gibt,
und wenn von diesem Zyklus aus ein Endzustand erreichbar ist.
genau dann, wenn es
in dem von Startzustand erreichbaren Teilgraphen einen Zyklus gibt,
und wenn von diesem Zyklus aus ein Endzustand erreichbar ist.
- wesentlich effizienter als erste Methode
Schnittproblem
Das Schnittproblem stellt bei gegebenen
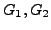 (bzw.
(bzw.
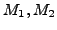 ) die Frage, ob
) die Frage, ob
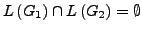 (bzw.
(bzw.
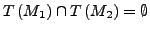 ). Hierfür
muss man eine Sprache (Grammatik) konstruieren, die aus
). Hierfür
muss man eine Sprache (Grammatik) konstruieren, die aus 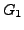 und
und
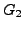 hervorgeht, und die beide Grammatiken sozusagen simultan
durchläuft. Hiermit ist dieses Problem auf das Leerheitsproblem zurückgeführt.
hervorgeht, und die beide Grammatiken sozusagen simultan
durchläuft. Hiermit ist dieses Problem auf das Leerheitsproblem zurückgeführt.
Äquivalenzproblem
Das Äquivalenzproblem stellt bei gegebene
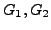 (bzw.
(bzw.
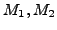 ) die Frage, ob
) die Frage, ob
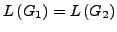 (bzw.
(bzw.
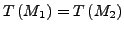 ). Hierzu gibt es
mehrere Lösungsmöglichkeiten:
). Hierzu gibt es
mehrere Lösungsmöglichkeiten:
- Per Minimalautomat:
- Wenn Sprachen nicht als DFA's vorliegen, diese dahingehend transformieren.
- Jeweils den Minimalautomaten konstruieren
- Diese auf Isomorphie (Umbenennung der Variablen) untersuchen, wenn
ja, dann sind die Sprachen gleich.
- Rückführung auf Leerheitsproblem:
Am Effizientesten ist die Methode des Minimalautomaten, wenn die Sprache
bereits als DFA vorliegt. Allgemein ist das Problem NP-hart,
hat also eine Laufzeitkomplexität von
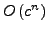 .
.





Next: Kontextfreie Sprachen (Typ 2)
Up: Reguläre Sprachen (Typ 3)
Previous: Abschlusseigenschaften 48
Contents
Index
Marco Möller 18:11:27 24.10.2005
![]() , gefragt: ist
, gefragt: ist
![]() bzw.
bzw.
![]() ) ist mit Hilfe eines DFA leicht möglich.
Verfolge einfach Zeichen für Zeichen die Zustandsübergänge im Automaten,
die durch die Eingabe
) ist mit Hilfe eines DFA leicht möglich.
Verfolge einfach Zeichen für Zeichen die Zustandsübergänge im Automaten,
die durch die Eingabe ![]() hervorgerufen werden. Falls ein Endzustand
erreicht wird, liegt
hervorgerufen werden. Falls ein Endzustand
erreicht wird, liegt ![]() in der Sprache. Die Laufzeitkomplexität
beträgt hier
in der Sprache. Die Laufzeitkomplexität
beträgt hier
![]() .
.
![]() (bzw.
(bzw. ![]() )
die Frage, ob
)
die Frage, ob
![]() (bzw.
(bzw.
![]() ).
Sei
).
Sei ![]() ein gegebener Automat für die Sprache.
ein gegebener Automat für die Sprache.
![]() ist genau dann leer, wenn es keinen Pfad vom (einem) Startzustand
zu einem Endzustand gibt.
ist genau dann leer, wenn es keinen Pfad vom (einem) Startzustand
zu einem Endzustand gibt.
![]() (bzw.
(bzw. ![]() )
die Frage, ob
)
die Frage, ob
![]() (bzw.
(bzw.
![]() ),
also ob die definierte Sprache endlich oder unendlich ist.
),
also ob die definierte Sprache endlich oder unendlich ist.
![]() (bzw.
(bzw.
![]() ) die Frage, ob
) die Frage, ob
![]() (bzw.
(bzw.
![]() ). Hierfür
muss man eine Sprache (Grammatik) konstruieren, die aus
). Hierfür
muss man eine Sprache (Grammatik) konstruieren, die aus ![]() und
und
![]() hervorgeht, und die beide Grammatiken sozusagen simultan
durchläuft. Hiermit ist dieses Problem auf das Leerheitsproblem zurückgeführt.
hervorgeht, und die beide Grammatiken sozusagen simultan
durchläuft. Hiermit ist dieses Problem auf das Leerheitsproblem zurückgeführt.
![]() (bzw.
(bzw.
![]() ) die Frage, ob
) die Frage, ob
![]() (bzw.
(bzw.
![]() ). Hierzu gibt es
mehrere Lösungsmöglichkeiten:
). Hierzu gibt es
mehrere Lösungsmöglichkeiten: