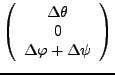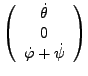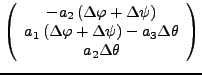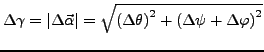Next: Spezielle Relativitätstheorie
Up: Grundlagen der Klassischen Mechanik
Previous: Kontinuierliche Systeme
Contents
Index
Subsections
Nicht Inertialsysteme
Transformation von Bezugssystemen
- Sachverhalt
- Sei ein Punkt bezüglich dem System
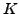 mit dem Vektor
mit dem Vektor
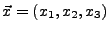 und bezüglich dem System
und bezüglich dem System
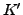 mit dem Vektor
mit dem Vektor
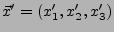 gegeben.
gegeben.
- Abstandserhaltend
- ist eine Abbildung dann,
wenn für zwei Punkte in beiden Systemen der gleiche Abstand gilt,
also
- Eine Transformation zwischen Bezugssystemen muss Abstandserhalten
geschehen
Transformation des Ortsvektors
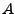 und
und 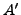 sind reelle orthoginale
sind reelle orthoginale 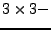 Matrizen. Das heißt
es gilt:
Matrizen. Das heißt
es gilt:
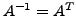
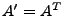
-
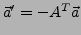
 bzw.
bzw.  sind die Abstände der Koordinatenursprünge
sind die Abstände der Koordinatenursprünge
- Es sind in der Summe
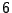 Parameter die die Transformation bestimmen.
Parameter die die Transformation bestimmen.
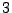 Winkel und
Winkel und 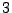 stück für den Offset Vektor.
stück für den Offset Vektor.
- die Strichgrössen
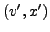 sind in den Koordinaten des
urspünglichen Systems einzugeben
sind in den Koordinaten des
urspünglichen Systems einzugeben
- Scheinkräfte
-
- Translative Kraft
-
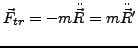
- Zentrifugalkraft
-
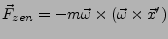
- Coreoliskraft
-
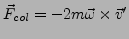
- Namenslos
-
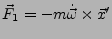
- Drehmatrix
-
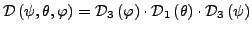
Figure 1:
Komplette Drehmatrize
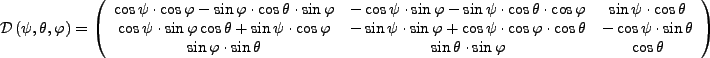 |
Eine Drehung des Vektors
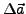 um den Winkel
um den Winkel 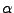 um die Achse
um die Achse
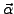 lässt sich durch das Kreuzprodukt
lässt sich durch das Kreuzprodukt
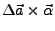 beschreiben
beschreiben





Next: Spezielle Relativitätstheorie
Up: Grundlagen der Klassischen Mechanik
Previous: Kontinuierliche Systeme
Contents
Index
Marco Möller 17:08:30 24.10.2005
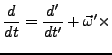
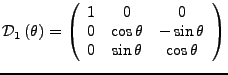
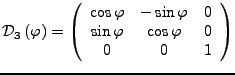
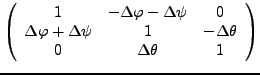
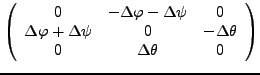
![]() um den Winkel
um den Winkel ![]() um die Achse
um die Achse
![]() lässt sich durch das Kreuzprodukt
lässt sich durch das Kreuzprodukt
![]() beschreiben
beschreiben