




Next: Harmonische Wellen
Up: Wellenbewegung in elastischen Medien
Previous: Wellenbewegung in elastischen Medien
Contents
Index
- Schwingung
- ein periodisch in der Zeit ablaufender
Vorgang
- Welle
- Zeit- und raumperiodischer Vorgang mit der Geschwindigkeit
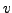
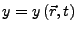
- Zugspannung
-

- Wellengleichung
-
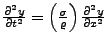
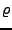 steht für die Materialdichte
steht für die Materialdichte
- Lösung Wellengleichung
-
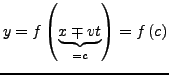 für welle in positive
für welle in positive 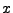 -Richtung steht dort ein
-Richtung steht dort ein  (Minus)!!
(Minus)!!
-
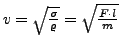
- bedeutet, dass an allen Stellen
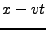
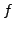 den gleichen Wert hat.
Da
den gleichen Wert hat.
Da 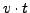 mit der Zeit wächst, rutsch der Ort, an dem
mit der Zeit wächst, rutsch der Ort, an dem 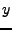 den
gleichen Wert hat in
den
gleichen Wert hat in 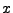 -Richtung davon.
-Richtung davon.
- Phase der Welle
-
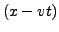
- Phasengeschwindigkeit
- Falls
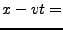 konstant
wird
konstant
wird 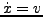 die Phasengeschwindigkeit genannt.
die Phasengeschwindigkeit genannt.
Marco Möller 16:43:44 24.10.2005
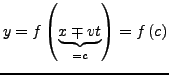 für welle in positive
für welle in positive