




Next: Verallgemeinerung der Zustandsgleichung der
Up: Wärmelehre
Previous: Wärmelehre
Contents
Index
- Ideales Gas
- Gase, die
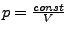 bei
bei 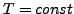 genügen heißen ideale Gase (z.B.
genügen heißen ideale Gase (z.B.
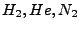 (Luft)),
dabei haben Gasteilchen kein eigenes Volumen (in sehr guter Näherung).
Außerdem wirken keine Abstossenden Kräfte (WW-Kräfte) zwischen ihnen.
(Luft)),
dabei haben Gasteilchen kein eigenes Volumen (in sehr guter Näherung).
Außerdem wirken keine Abstossenden Kräfte (WW-Kräfte) zwischen ihnen.
- reale Gase
- sind Gase, die
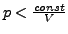 bei
bei 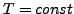 genügen (z.B.
genügen (z.B. 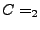 ). Das heisst, das der Druck
kleiner ist als bei einem idelaen Gas, wegen der WW-Kräfte der Gasmoleküle
untereinander
). Das heisst, das der Druck
kleiner ist als bei einem idelaen Gas, wegen der WW-Kräfte der Gasmoleküle
untereinander
- Boyle-Mariotte'sches Gesetz
-
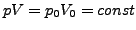 bei Temperatur
bei Temperatur 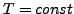
- Über Dichte Ausgedrückt
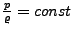
-
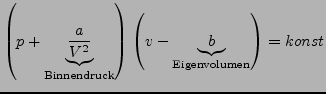 bei
bei 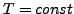
 van der Waalsche Konstanten
van der Waalsche Konstanten
- Gay-Lussare'sche Gesetz
-
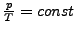 bei
bei 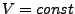
- Zustandsgleichung des idealen Gases
-
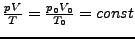
- Zustandsdiagramme
- es gibt 3 Schnittlinien
der Zustandsfläche mit der Ebene
- Isotherme
- für
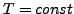 . Ergibt im
. Ergibt im 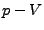 Diagramm
Hyperbeln, die für Größere
Diagramm
Hyperbeln, die für Größere 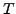 weiter von den Achsen entfernt sind
weiter von den Achsen entfernt sind
- Isobare
- für
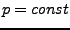 . Ergibt Ursprungsgraden im
. Ergibt Ursprungsgraden im
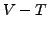 Diagramm, mit größerer Steigung für kleinere
Diagramm, mit größerer Steigung für kleinere 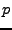
- Isochore
- für
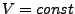 . Ergibt Ursprungsgraden
im
. Ergibt Ursprungsgraden
im 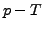 Diagramm, mit größerer Steigung für kleinere
Diagramm, mit größerer Steigung für kleinere 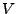
- Grad Celsius
- Temperatureinteilung,
mit
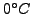 bei Gefrierpunkt von Wasser und
bei Gefrierpunkt von Wasser und 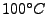 bei Siedepunkt
von Wasser unter Normalbedingungen von
bei Siedepunkt
von Wasser unter Normalbedingungen von 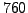 Torr.
Torr.
- Kelvin
- Gleiche Abstufung wie bei Grad Celsius, aber
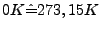
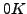 ist die absolute Temperatur,
das heist, dass es keine kältere Temperaturen geben kann.
ist die absolute Temperatur,
das heist, dass es keine kältere Temperaturen geben kann.
- bei
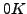 befinden sich die Molekühle in absoluter Ruhe
befinden sich die Molekühle in absoluter Ruhe
- Trippelpunkt
- des Wassers. Bei
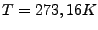 und
und 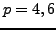 Torr kommt Wasser in allen 3 Phasen (fest, flüssig, gasförmig)
gleichzeitig vor. In diesem Punkt schneiden sich die 3 Übergangslinien
zwischen jeweils zwei Agregatszuständen.
Torr kommt Wasser in allen 3 Phasen (fest, flüssig, gasförmig)
gleichzeitig vor. In diesem Punkt schneiden sich die 3 Übergangslinien
zwischen jeweils zwei Agregatszuständen.
- Temperaturabhängiger Widerstand
- für nicht sehr kalte Temperaturen
gilt:
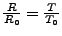





Next: Verallgemeinerung der Zustandsgleichung der
Up: Wärmelehre
Previous: Wärmelehre
Contents
Index
Marco Möller 16:43:44 24.10.2005
 bei
bei