




Next: QM in Dimensionen
Up: Formalisierung der Quantenmechanik
Previous: Formalisierung der Quantenmechanik
Contents
Index
Subsections
Funktionenräume
- Vektoren
-
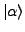 entspricht einer Funktionen
entspricht einer Funktionen
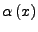 . Diese Funktionen bilden einen
. Diese Funktionen bilden einen
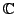 Vektorraum.
Vektorraum.
- Lineare Abbildungen
- Sind lineare Operatoren
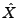 . Diese sind im endlichdimensionalen mit Matrizen vergleichbar
. Diese sind im endlichdimensionalen mit Matrizen vergleichbar
- Bsp:
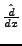 in Polynomen vom Grad
in Polynomen vom Grad 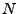 ,
, 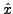 im formaten Potenzreihen
im formaten Potenzreihen
- Eigenfunktion
-
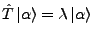
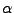 heißt Eigenfunktion zum Eigenwert
heißt Eigenfunktion zum Eigenwert 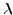 von
von 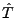
- Skalarprodukt
-
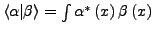 dx
dx
- Die Grenzen müssen Passend zu Problem definiert werden
- Funktionen müssen Quadratintegrable sein
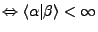
- hermitesche Operatoren
-
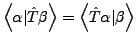 für alle
für alle
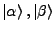
Hilbertraum
In der QM sind wir an Fkt. interressiert, die quadrat-integrabel sind
Der Raum der von solchen Funktionen aufgespannt wird, wird mit
bezeichnet.
Ein Vektorraum 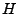 mit einem inneren Produckt,
mit einem inneren Produckt,
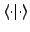 heißt Hilbertraum, falls alle Konvergenten Reihen in
heißt Hilbertraum, falls alle Konvergenten Reihen in 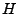 gegen einen
Vektor in
gegen einen
Vektor in 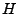 konvergieren (Vollständig).
konvergieren (Vollständig).
- Ein Teilchen wird repräsentiert durch eine Wellenfunktion
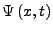
-
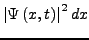 ist die Warscheinlichkeit,
das Teilchen im Intervall
ist die Warscheinlichkeit,
das Teilchen im Intervall
![$ \left[x,x+dx\right]$](img247.png) zur Zeit
zur Zeit 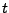 zu
finden
zu
finden
- Die Normierung muss erfüllt sein:
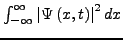
Dann haben wir
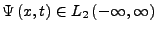 mit dem inneren Produkt
mit dem inneren Produkt
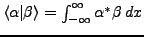
- Wir Identifizieren ein Teilchen mit einem Vektor in
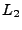 und bezeichnen
es als
und bezeichnen
es als
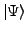 . Die Normierung fordert
. Die Normierung fordert
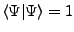
- Meßgrößen sind hermitesche Operatoren
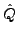 . Der Erwartungswert
von
. Der Erwartungswert
von 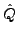 ist
ist
- Messungen von Observablen liefern die Eigenwerte (reellen) von
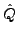 und zwingen das System einen Eigenzustand anzunehmen
und zwingen das System einen Eigenzustand anzunehmen
- Die Varianz der Messung ist
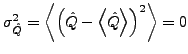 genau dann , wenn sich das System in einem Eigenzustand von
genau dann , wenn sich das System in einem Eigenzustand von 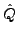 befindet.
befindet.
-
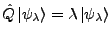 bestimmen des Eigenspektrum (Menge der Eigenwerte) mit den zugehörigen
Eigenvektoren
bestimmen des Eigenspektrum (Menge der Eigenwerte) mit den zugehörigen
Eigenvektoren
- Bilden einer Orthonormalbasis aus den
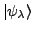
- Ein belibiger Zustand ist aus aus Basis linear kombinierbar
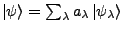 ,
,
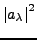 ist die Wahrscheinlichkeit
ist die Wahrscheinlichkeit 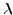 bei einer Messung von
bei einer Messung von 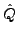 in
in
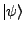 zu
finden.
zu
finden.
Projektor / Basiswechsel
- Einsoperator
-
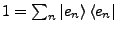
- Falls
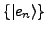 eine Vollständige,
orthonormierte Basis bilden
eine Vollständige,
orthonormierte Basis bilden
- Projektor
- ist ein Operator, für den gilt
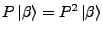
- Eigenwerte
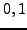
- Zerlegung
-
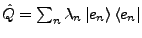
- Jeder hermitesche Operator lässt sich auf ``Diagonalgestalt''
bringen
diskretes Spektrum
- Vollständigkeit
-
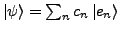
- Wahrscheinlichkeit
- dass
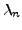 Auftritt
Auftritt
kontinuierliches Spektrum
- Eigenzustände
-
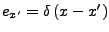
- Eigenwertgleichung
-
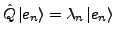 mit
mit 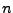 kontinuierlich und
kontinuierlich und
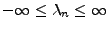
- Othogonale Basis
-
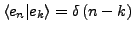
- Vollständigkeit
-
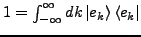
- Wahrscheinlichkeitsdichte
-
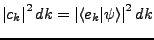
- Fourier Transformation
-
damit gilt
- Mittelwerte
- von Kontinuierlichen Spektren
Heisenberg's Unschärfe
- nicht vom gleichen Typ wie
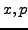 Unschärfe, weil
Unschärfe, weil 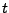 keine Observable
ist.
keine Observable
ist.





Next: QM in Dimensionen
Up: Formalisierung der Quantenmechanik
Previous: Formalisierung der Quantenmechanik
Contents
Index
Marco Möller 21:20:46 15.11.2006
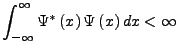
![]() mit einem inneren Produckt,
mit einem inneren Produckt,
![]() heißt Hilbertraum, falls alle Konvergenten Reihen in
heißt Hilbertraum, falls alle Konvergenten Reihen in ![]() gegen einen
Vektor in
gegen einen
Vektor in ![]() konvergieren (Vollständig).
konvergieren (Vollständig).
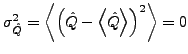 genau dann , wenn sich das System in einem Eigenzustand von
genau dann , wenn sich das System in einem Eigenzustand von 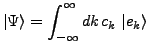
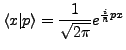
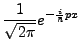
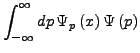
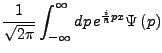
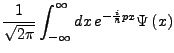
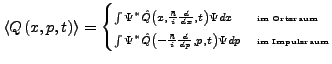
![$\displaystyle \sigma_{\hat{A}}^{2}\sigma_{\hat{B}}^{2}\ge\left(\frac{1}{2i}\left\langle \left[\hat{A},\hat{B}\right]\right\rangle \right)^{2}$](img293.png)
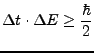
![$\displaystyle \frac{d}{dt}\left\langle \hat{Q}\right\rangle =\frac{i}{\hbar}\le...
...ht]\right\rangle +\left\langle \frac{\partial\hat{Q}}{\partial t}\right\rangle $](img308.png)