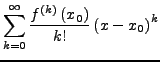Next: Funktionen mehrerer Veränderlicher II.199
Up: Taylorentwicklung II.141
Previous: Satz von Taylor II.141
Contents
Index
Taylorreihe II.152
Sei
![$ f\left[a,b\right]\rightarrow\mathbb{R}$](img703.png) beliebig oft differenzierbar,
und
beliebig oft differenzierbar,
und
![$ x\in\left[a,b\right]$](img370.png) . Die Reihe
. Die Reihe
heißt Taylorreihe von  um
um 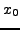 . Sie konvergiert an
. Sie konvergiert an 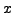 genau
dann gegen
genau
dann gegen
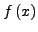 wenn
wenn
- Nicht jede Taylorreihe konvergiert
- Konvergenz kann evt. nur für Intervalle bestehen
- wichtige Reihen siehe sub:Besondere-Reihen und sub:wichtige-Reihen-II.154.
Marco Möller 17:42:11 24.10.2005
![]() beliebig oft differenzierbar,
und
beliebig oft differenzierbar,
und
![]() . Die Reihe
. Die Reihe