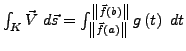Sei
![]() eine stetige
differenzierbare Funktion und
eine stetige
differenzierbare Funktion und
![]() für
für
![]() .
.
Dann heißt ![]() und die Punktmenge
und die Punktmenge
![]() eine glatte Kurve.
eine glatte Kurve. ![]() heißt Parameter
der Kurve,
heißt Parameter
der Kurve,
![]() Parameterintervall.
Parameterintervall.
![]() heißt stückweise glatt, wenn
es in den Teilintervallen einer Zerlegung
heißt stückweise glatt, wenn
es in den Teilintervallen einer Zerlegung
![]() glatt ist, und somit stetig.
glatt ist, und somit stetig.
Eine Kurve
![]() heißt geschlossen, wenn
heißt geschlossen, wenn
![]() .
Ist
.
Ist ![]() injektiv auf
injektiv auf
![]() , so heißt
, so heißt ![]() doppelpunktfrei.
doppelpunktfrei.
Durch
![]() ,
,
![]() werde jeweils eine stückweise glatte Kurve dargestellt. Weiter existiere
eine stetig differenzierbare Funktion
werde jeweils eine stückweise glatte Kurve dargestellt. Weiter existiere
eine stetig differenzierbare Funktion
![]() mit
mit
![]() ,
,
![]() und
und
![]() für alle
für alle
![]() , und es
gelte
, und es
gelte
Sei ![]() eine Stückweise glatte Kurve, die durch
eine Stückweise glatte Kurve, die durch
![]() dargestellt werde. Der Vektor
dargestellt werde. Der Vektor
![]() heißt Tangentenvektor
an
heißt Tangentenvektor
an ![]() im Punkt
im Punkt
![]() ,
,
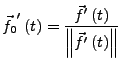
Durch ![]() werde eine glatte, doppelpunktfreie Kurve
werde eine glatte, doppelpunktfreie Kurve ![]() dargestellt.
Das Integral
dargestellt.
Das Integral
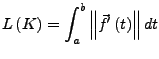
Sei ![]() eine glatte doppelpunktfreie Kurve, die durch
eine glatte doppelpunktfreie Kurve, die durch
![]() gegeben sei. Dann heißt die Funktion
gegeben sei. Dann heißt die Funktion
![]() ,
erklärt durch
,
erklärt durch
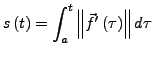
Sei ![]() eine glatte doppelpunktfreie Kurve. Die Bogenlänge
eine glatte doppelpunktfreie Kurve. Die Bogenlänge ![]() ist
eine stetige, differenzierbare, streng monoton wachsende Funktion
und besitzt eine Umkehrfunktion
ist
eine stetige, differenzierbare, streng monoton wachsende Funktion
und besitzt eine Umkehrfunktion ![]() mit denselben Eigenschaften.
Die Parameterdarstellung
mit denselben Eigenschaften.
Die Parameterdarstellung
![]() ,
,
![]() ist zur gegebenen Darstellung
ist zur gegebenen Darstellung
![]() äquivalent, und es gilt
äquivalent, und es gilt
Eine auf einer offenen Teilmenge
![]() erklärte,
stetig differenzierbare Funktion
erklärte,
stetig differenzierbare Funktion
![]() nennen wir ein Vektorfeld. Entsprechend
heißt
nennen wir ein Vektorfeld. Entsprechend
heißt
![]() ein Skalarfeld.
ein Skalarfeld.
Sei
![]() offen,
offen,
![]() ein Vektorfeld. Sei
ein Vektorfeld. Sei ![]() eine durch
eine durch
![]() gegebene stückweise glatte Kurve. Dann heißt
gegebene stückweise glatte Kurve. Dann heißt
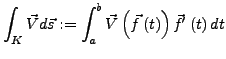
Ein Vektorfeld
![]() heißt Potentialfeld,
falls es eine Funktion
heißt Potentialfeld,
falls es eine Funktion
![]() mit
mit
![]() gibt.
gibt.
![]() heißt konvex
heißt konvex
![]() mit je zwei Punkten
mit je zwei Punkten
![]() gehört auch die
Verbindungsgrade
gehört auch die
Verbindungsgrade
![]() zu
zu ![]() .
.
Sei
![]() offen und konvex und
offen und konvex und
![]() ein Vektorfeld. Dann gilt: Das Kurvenintegral
ein Vektorfeld. Dann gilt: Das Kurvenintegral
![]() ist wegunabhängig
ist wegunabhängig
![]()
![]() ist ein Potentialfeld.
ist ein Potentialfeld.
Sei
![]() stetig. Dann wird durch
stetig. Dann wird durch
![]() ein Vektorfeld auf
ein Vektorfeld auf
![]() gegeben. Man bezeichnet solche Felder als Zentralfeld.
gegeben. Man bezeichnet solche Felder als Zentralfeld.