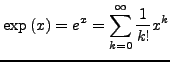Es sei
![]() eine Folge. Setze
eine Folge. Setze
![]() .
Diese neue Folge
.
Diese neue Folge
![]() heißt Partialsummenfolge
oder unendliche Reihe, schreibe
heißt Partialsummenfolge
oder unendliche Reihe, schreibe
![]() .
Falls diese Folge
.
Falls diese Folge
![]() konvergiert,
spricht mann von einer konvergenten Reihe,
ansonsten von einer divergenten Reihe.
Für den Grenzwert
konvergiert,
spricht mann von einer konvergenten Reihe,
ansonsten von einer divergenten Reihe.
Für den Grenzwert
![]() schreibe
schreibe
![]() .
.
Eine Reihe
![]() konvergiert genau dann, wenn
die Folge
konvergiert genau dann, wenn
die Folge
![]() ihrer Partialsummen
eine Cauchy-Folge ist. D.h. die Reihe konvergiert genau dann, wenn
es zu jedem
ihrer Partialsummen
eine Cauchy-Folge ist. D.h. die Reihe konvergiert genau dann, wenn
es zu jedem
![]() ein
ein
![]() gibt, so dass
gibt, so dass
![]() für alle
für alle
![]() . Mit Quantoren:
. Mit Quantoren:
![]() ist konvergent
ist konvergent
![]()
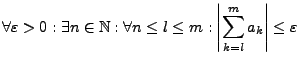
Ist
![]() eine streng monoton fallende
Nullfolge. Dann konvergiert die Reihe
eine streng monoton fallende
Nullfolge. Dann konvergiert die Reihe
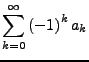
Eine Reihe
![]() konvergiert absolut,
falls die Reihe
konvergiert absolut,
falls die Reihe
![]() konvergiert.
Jede absolut konvergente Reihe konvergiert.
konvergiert.
Jede absolut konvergente Reihe konvergiert.
Sind
![]() und
und
![]() Folgen, und gilt
Folgen, und gilt
![]() für fast alle
für fast alle
![]() , so
haben die beiden Folgen
, so
haben die beiden Folgen
![]() ,
,
![]() und die beiden Reihen
und die beiden Reihen
![]() und
und
![]() das gleiche Konvergenzverhalten
das gleiche Konvergenzverhalten
Sind
![]() und
und
![]() Reihen
mit
Reihen
mit
![]() für fast alle
für fast alle ![]() ,
und wenn
,
und wenn
![]() absolut konvergiert, dann konvergiert
auch
absolut konvergiert, dann konvergiert
auch
![]() absolut.
absolut.
Ist
![]() eine Reihe, und gibt es
eine Reihe, und gibt es
![]() mit
mit
![]() so dass für fast alle
so dass für fast alle ![]() gilt
gilt
![]() .
Dann konvergiert die Reihe absolut. Ist jedoch
.
Dann konvergiert die Reihe absolut. Ist jedoch
![]() eine unendliche Menge divergiert die Reihe. Ansonsten lassen sich
keine Aussagen machen.
eine unendliche Menge divergiert die Reihe. Ansonsten lassen sich
keine Aussagen machen.
Gibt es ein
![]() mit
mit ![]() so, dass
so, dass
![]() für fast alle
für fast alle ![]() , dann konvergiert die Reihe
, dann konvergiert die Reihe
![]() absolut.
absolut.
Sei
![]() eine positive, monoton fallende Folge.
Dann gilt:
eine positive, monoton fallende Folge.
Dann gilt:
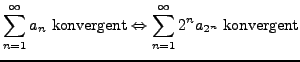
Sind
![]() und
und
![]() konvergent,
so auch
konvergent,
so auch
![]() , mit dem Grenzwert
, mit dem Grenzwert
![]() .
.
Sind
![]() und
und
![]() Reihen,
definieren wir ihr Cauchy-Produkt
Reihen,
definieren wir ihr Cauchy-Produkt
![]() durch
durch
![]() .
.
Sind
![]() und
und
![]() absolut
konvergent, dann ist ihr Cauch-Produkt ebenfalls absolut konvergent
und im Grenzwert gilt:
absolut
konvergent, dann ist ihr Cauch-Produkt ebenfalls absolut konvergent
und im Grenzwert gilt:
![]() .
.