Next: Integral
Up: Integration
Previous: Integration
Contents
Index
Subsections
Sei
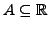 . Eine Funktion
. Eine Funktion
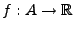 heißt beschränkt, falls
heißt beschränkt, falls
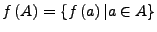 beschränkt ist. D.h. falls es eine Zahl
beschränkt ist. D.h. falls es eine Zahl
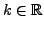 gibt, so
dass
gibt, so
dass
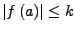 für alle
für alle 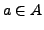 .
.
Sei
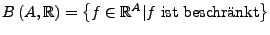 die Menge aller beschränkten Funktionen.
die Menge aller beschränkten Funktionen.
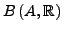 ist ein reeller Vektorraum und ein Ring,
d.h. es gilt
ist ein reeller Vektorraum und ein Ring,
d.h. es gilt
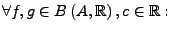
-
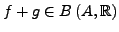
-
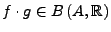
-
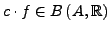
- Ist der Definitionsbereich ein endliches abgeschlossenes Intervall,
dann gilt
![$ C\left(\left[a,b\right],\mathbb{R}\right)\subsetneq B\left(\left[a,b\right],\mathbb{R}\right)$](img655.png) .
D.h. dass die stetigen Funktionen eine (echte) Teilmenge der beschränkten
Funktionen sind.
.
D.h. dass die stetigen Funktionen eine (echte) Teilmenge der beschränkten
Funktionen sind.
Für
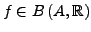 setzte
setzte
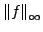 heißt (Supremums-)Norm
der Funktion
heißt (Supremums-)Norm
der Funktion  .
.
-
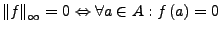
- Dreiecksungleichung
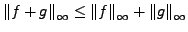
-
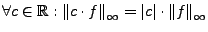
-
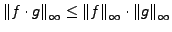
-
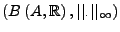 ist
ein normierter Vektorraum
und sogar eine normierte Algebra
dank der Produkteigenschaft der Norm.
ist
ein normierter Vektorraum
und sogar eine normierte Algebra
dank der Produkteigenschaft der Norm.
gleichmäßige Konvergenz
Ist
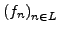 eine Folge von Funktionen in
eine Folge von Funktionen in
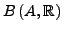 ,
so konvergiert diese Folge gleichmäßig gegen
,
so konvergiert diese Folge gleichmäßig gegen
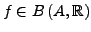 genau dann, wenn gilt
genau dann, wenn gilt
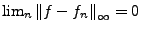 .
.
Eine Folge
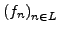 in
in
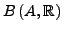 heißt Cauchy-Folge, falls gilt: Zu jedem
heißt Cauchy-Folge, falls gilt: Zu jedem
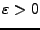 gibt es ein
gibt es ein
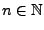 , so dass
, so dass
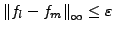 für alle
für alle 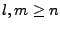 .
.
- Eine Folge
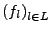 in
in
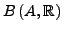 ist genau dann eine Cauchyfolge, wenn sie gegen eine Funktion
ist genau dann eine Cauchyfolge, wenn sie gegen eine Funktion
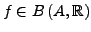 gleichmäßig konvergiert.
gleichmäßig konvergiert.
- Im normierten Raum
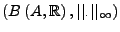 konvergiert jede Cauchyfolge. Man nennt den Raum daher vollständig
oder Banachraum.
konvergiert jede Cauchyfolge. Man nennt den Raum daher vollständig
oder Banachraum.
Eine Zerlegung 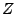 von
von
![$ \left[a,b\right]$](img669.png) ist eine enliche Folge
ist eine enliche Folge
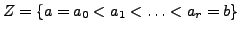 .
Eine andere Zerlegung
.
Eine andere Zerlegung 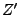 heißt feiner als
heißt feiner als
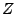 falls
falls
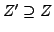 .
.
- Falls
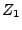 und
und 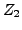 Zerlegungen von
Zerlegungen von
![$ \left[a,b\right]$](img669.png) sind,
so auch
sind,
so auch
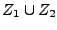 , welche feiner ist als
, welche feiner ist als 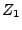 und
und 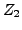 .
.
Eine Funktion
![$ f\in B\left(\left[a,b\right],\mathbb{R}\right)$](img676.png) heißt
Stufenfunktion (bzgl. Zerlegung
heißt
Stufenfunktion (bzgl. Zerlegung 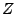 )
falls
)
falls
Die Menge aller Stufenfunktionen wird mit
![$ \textrm{Step}\left(\left[a,b\right],\mathbb{R}\right)\subsetneq B\left(\left[a,b\right],\mathbb{R}\right)$](img678.png) bezeichnet.
bezeichnet.
- Falls
 eine Stufenfunktion bzgl.
eine Stufenfunktion bzgl. 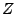 ist, und falls
ist, und falls 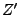 feiner
als
feiner
als 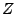 ist, dann ist
ist, dann ist  auch Stufenfunktion bzgl.
auch Stufenfunktion bzgl. 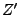
- Eine Stufenfunktion muss endlich viele Stufen haben
- Ist
 Stufenfunktion bzgl.
Stufenfunktion bzgl. 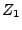 und
und 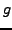 Stufenfunktion bzgl.
Stufenfunktion bzgl.
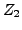 , dann sind
, dann sind 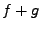 ,
, 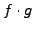 und
und 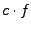 (für
(für
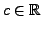 )
Stufenfunktionen bzgl.
)
Stufenfunktionen bzgl.
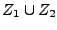 .
.
-
![$ \textrm{Step}\left(\left[a,b\right],\mathbb{R}\right)<B\left(\left[a,b\right],\mathbb{R}\right)$](img683.png) ist Untervektorraum der beschränkten Funktionen. Außerdem ist diese
Menge ein Ring. Somit also eine Algebra.
ist Untervektorraum der beschränkten Funktionen. Außerdem ist diese
Menge ein Ring. Somit also eine Algebra.
- Die Einschränkung einer Stufenfunktion ist wieder eine Stufenfunktion.
Ist
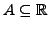 eine Teilmenge der reellen Zahlen, so
heißt die Funktion
eine Teilmenge der reellen Zahlen, so
heißt die Funktion
die charakteristische Funktion
der Menge  .
.





Next: Integral
Up: Integration
Previous: Integration
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() . Eine Funktion
. Eine Funktion
![]() heißt beschränkt, falls
heißt beschränkt, falls
![]() beschränkt ist. D.h. falls es eine Zahl
beschränkt ist. D.h. falls es eine Zahl
![]() gibt, so
dass
gibt, so
dass
![]() für alle
für alle ![]() .
.
![]() ist ein reeller Vektorraum und ein Ring,
d.h. es gilt
ist ein reeller Vektorraum und ein Ring,
d.h. es gilt
![]()
![]() setzte
setzte
![]() heißt (Supremums-)Norm
der Funktion
heißt (Supremums-)Norm
der Funktion ![]() .
.
![]() eine Folge von Funktionen in
eine Folge von Funktionen in
![]() ,
so konvergiert diese Folge gleichmäßig gegen
,
so konvergiert diese Folge gleichmäßig gegen
![]() genau dann, wenn gilt
genau dann, wenn gilt
![]() .
.
![]() in
in
![]() heißt Cauchy-Folge, falls gilt: Zu jedem
heißt Cauchy-Folge, falls gilt: Zu jedem
![]() gibt es ein
gibt es ein
![]() , so dass
, so dass
![]() für alle
für alle ![]() .
.
![]() von
von
![]() ist eine enliche Folge
ist eine enliche Folge
![]() .
Eine andere Zerlegung
.
Eine andere Zerlegung ![]() heißt feiner als
heißt feiner als
![]() falls
falls
![]() .
.
![]() heißt
Stufenfunktion (bzgl. Zerlegung
heißt
Stufenfunktion (bzgl. Zerlegung ![]() )
falls
)
falls
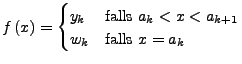
![]() bezeichnet.
bezeichnet.
![]() eine Teilmenge der reellen Zahlen, so
heißt die Funktion
eine Teilmenge der reellen Zahlen, so
heißt die Funktion