




Next: Zusammenhang von Differential- und
Up: Die Hauptsätze der Differential-
Previous: Die Hauptsätze der Differential-
Contents
Index
Subsections
Integral über Einschränkung
Ist
![$ f:\left[a,b\right]\rightarrow\mathbb{R}$](img514.png) Regelfunktion und
Regelfunktion und
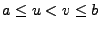 .
Dann ist die Einschränkung
.
Dann ist die Einschränkung
![$ f\vert _{\left[u,v\right]}$](img833.png) eine Regelfunktion
auf
eine Regelfunktion
auf
![$ \left[u,v\right]$](img834.png) . Wir setzen
. Wir setzen
Wir legen fest:
Zerteilung von Integralen
Für alle
![$ a,b,c\in\left[a,c\right]$](img838.png) und
und
![$ f\in R\left(\left[a,c\right],\mathbb{R}\right)$](img839.png) gilt stets
gilt stets
Integral über Funktionsfolge
Sei
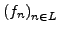 eine Folge von Regelfunktionen,
die gleichmäßig gegen eine Regelfunktion
eine Folge von Regelfunktionen,
die gleichmäßig gegen eine Regelfunktion  konvergiert. Dann gilt
konvergiert. Dann gilt
- eine solche Regel gilt bei der Differentiation im Allgemeinen nicht.
Sei
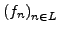 Folge in
Folge in
![$ C^{1}\left(\left[a,b\right],\mathbb{R}\right)$](img842.png) .
Falls die Folge
.
Falls die Folge
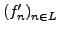 gleichmäßig konvergiert
und falls die Folge
gleichmäßig konvergiert
und falls die Folge
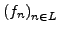 punktweise konvergiert,
dann ist der Grenzwert der Folge stetig differenzierbar und seine
Ableitung ist der Grenzwert der Folge
punktweise konvergiert,
dann ist der Grenzwert der Folge stetig differenzierbar und seine
Ableitung ist der Grenzwert der Folge
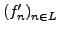 .
.
gerade und ungerade Funktionen
- Die Stammfunktion einer geraden Funktion ist eine ungerade Funktion
- Die Stammfunktion einer ungeraden Funktion ist eine gerade Funktion
- wenn
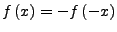 ungerade ist, gilt
ungerade ist, gilt
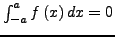





Next: Zusammenhang von Differential- und
Up: Die Hauptsätze der Differential-
Previous: Die Hauptsätze der Differential-
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() Regelfunktion und
Regelfunktion und
![]() .
Dann ist die Einschränkung
.
Dann ist die Einschränkung
![]() eine Regelfunktion
auf
eine Regelfunktion
auf
![]() . Wir setzen
. Wir setzen
![$\displaystyle \int_{u}^{v}f\left(x\right)dx=\int_{a}^{b}f\vert _{\left[u,v\right]}\left(x\right)dx$](img835.png)
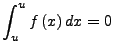
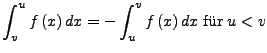
![]() und
und
![]() gilt stets
gilt stets
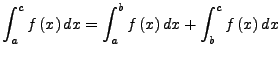
![]() eine Folge von Regelfunktionen,
die gleichmäßig gegen eine Regelfunktion
eine Folge von Regelfunktionen,
die gleichmäßig gegen eine Regelfunktion ![]() konvergiert. Dann gilt
konvergiert. Dann gilt
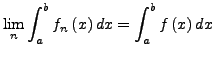
![]() Folge in
Folge in
![]() .
Falls die Folge
.
Falls die Folge
![]() gleichmäßig konvergiert
und falls die Folge
gleichmäßig konvergiert
und falls die Folge
![]() punktweise konvergiert,
dann ist der Grenzwert der Folge stetig differenzierbar und seine
Ableitung ist der Grenzwert der Folge
punktweise konvergiert,
dann ist der Grenzwert der Folge stetig differenzierbar und seine
Ableitung ist der Grenzwert der Folge
![]() .
.