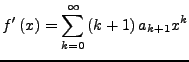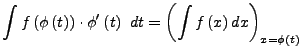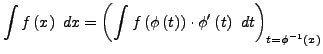Next: Metrische und nomierte Räume
Up: Die Hauptsätze der Differential-
Previous: Weitere Eigenschaften des Integrals
Contents
Index
Subsections
1. Hauptsatz der
Differential- und Integralrechung
Es sei
![$ f:\left[a,b\right]\rightarrow\mathbb{R}$](img514.png) stetig, sei
stetig, sei
![$ x_{0}\in\left[a,b\right]$](img846.png) .
Setze
.
Setze
für
![$ x\in\left[a,b\right]$](img704.png) .
.
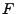 ist stetig und auf
ist stetig und auf
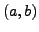 stetig differenzierbar,
mit
stetig differenzierbar,
mit 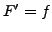 .
.
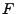 heißt Stammfunktion zu
heißt Stammfunktion zu  , falls
, falls
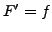 .
.
- Stammfunktionen sind bis auf Konstante eindeutig. Wenn
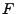 Stammfunktion
von
Stammfunktion
von  ist, ist auch
ist, ist auch 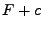 Stammfunktion für
Stammfunktion für  mit
mit
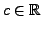 konstant.
konstant.
2. Hauptsatz der
Differential- und Integralrechung
Ist
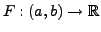 stetig differenzierbar
und
stetig differenzierbar
und 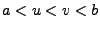 , gilt
, gilt
Integral einer Potenzreihe
Ist
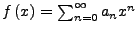 und hat diese
Potenzreihe einen Konvergenzradius
und hat diese
Potenzreihe einen Konvergenzradius 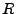 . Für
. Für
![$ \left[a,b\right]\subseteq\left(-R,R\right)$](img855.png) gilt
gilt
- Eine Stammfunktion für
 ist also z.B.
ist also z.B.
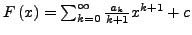
- Potenzreihen darf man ``naiv'' integrieren
Ist
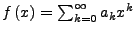 Potenzreihe mit
Konvergenzradius
Potenzreihe mit
Konvergenzradius 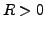 , so ist
, so ist  glatt, und
glatt, und
mit dem gleichen Konvergenzradius 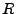 .
.
- Potenzreihen darf man ``naiv'' ableiten
Partielle Integration
Integration durch Substitution
- Gebrauchsanweisung
- Eine passende Ersetzung suchen
-
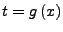
- diese Ableiten
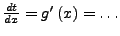
- umstellen
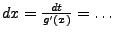
- Im Integral Substituieren mit Hilfe von (a).i (bzw.
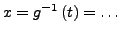 )
und (a).iii
)
und (a).iii
- Versuchen Stammfunktion zu bilden
- wenn es nicht klappt, evtl. andere Substitution versuchen
- evtl. passend klammern, um bekannte Integrale zu Nutzen
- Im Ergebnis (Stammfunktion) zurücksubstituieren mit (a).i
- Gebrauchsanweisung
- Eine passende Ersetzung suchen
-
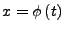
- diese Ableiten
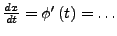
- umstellen
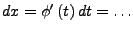
- Umkehrfunktion bilden
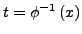
- Im Integral Subtituieren mit Hilfe von (a).i und (a).iii
- Versuchen Stammfunktion zu bilden
- wenn es nicht klappt, evtl. andere Substitution versuchen
- evtl. passend klammern, um bekannte Integrale zu Nutzen
- Im Ergebnis (Stammfunktion) zurücksubstituieren mit (a).i
- Beide Methoden äquivalent durch Regel der Ableitung der Umkehrfunktion.
- In der Tabelle cap:Substitution-unbestimmten-Int hat man eine
Übersicht von geeigneten Substitutionen.
- So Klammern und Substituieren, das es auf etwas bekanntes (z.B. Ableitungen
von Trigonometrischen-, Hyperbolischen- oder Areafunktioen) zurückführen
lässt.
- Auf jeden Fall Probe!!!





Next: Metrische und nomierte Räume
Up: Die Hauptsätze der Differential-
Previous: Weitere Eigenschaften des Integrals
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() stetig, sei
stetig, sei
![]() .
Setze
.
Setze
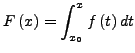
![]() ist stetig und auf
ist stetig und auf
![]() stetig differenzierbar,
mit
stetig differenzierbar,
mit ![]() .
.
![]() heißt Stammfunktion zu
heißt Stammfunktion zu ![]() , falls
, falls
![]() .
.
![]() stetig differenzierbar
und
stetig differenzierbar
und ![]() , gilt
, gilt
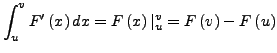
![]() und hat diese
Potenzreihe einen Konvergenzradius
und hat diese
Potenzreihe einen Konvergenzradius ![]() . Für
. Für
![]() gilt
gilt
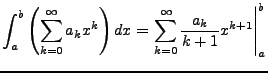
![]() Potenzreihe mit
Konvergenzradius
Potenzreihe mit
Konvergenzradius ![]() , so ist
, so ist ![]() glatt, und
glatt, und