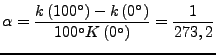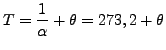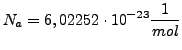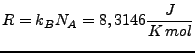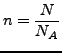Next: Reale Gase
Up: Thermodynamik
Previous: Themperaturegriff
Contents
Index
Subsections
Ideales Gas
- Punktteilchen: kein Eigenvolumen
- keine Wechselwirkung
- entsprechen Realen Gasen unter extremer Verdünnung
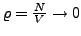
Nach Boyle-Mariott gilt
gemäß der Erfahrung gilt:
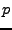 Druck, Kraft pro Fläche
Druck, Kraft pro Fläche
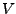 Volumen
Volumen
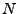 Anzahl Teilchen im Volumen
Anzahl Teilchen im Volumen
Celsius Skala
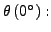 Gefrierpunkt von Wasser bei
Gefrierpunkt von Wasser bei 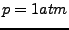
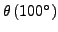 : Siedepunkt von Wasser bei
: Siedepunkt von Wasser bei 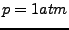
Kelvin Skala
Dies ist eine Absolute Temperaturskala. D.h. es gibt keine negativen
Temperaturen.
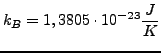
mit der Bolzmann Konstante
Somit gilt für das ideale Gaß
mit der Avogrado-Konstante
und der Idealen Gaskonstante
und der Molanzahl 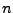
lässt sich die ideale Gasgleichung auch so schreiben
- Diese Gleichung kann keine Phasenübergänge beschreiben





Next: Reale Gase
Up: Thermodynamik
Previous: Themperaturegriff
Contents
Index
Marco Möller 17:08:30 24.10.2005
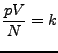
![]() Gefrierpunkt von Wasser bei
Gefrierpunkt von Wasser bei ![]()
![]() : Siedepunkt von Wasser bei
: Siedepunkt von Wasser bei ![]()