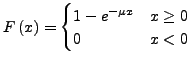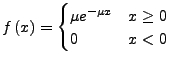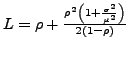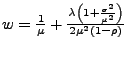Next: Petrinetze
Up: Diskrete Modellierung und Simulation
Previous: DEVS
Contents
Index
Subsections
Grundbegriffe Statistik
- Zufallsgröße
-
- Wahrscheinlichkeit
-
![$ Pr\left[\underbar{x}\le x\right]$](img17.png) das
das
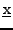 kleiner oder gleich
kleiner oder gleich 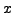
- Verteilungsfunktion
-
![$ F\left(x\right)=Pr\left[\underbar{x}\le x\right]$](img19.png)
- Stetige Verteilung
- falls der Wertebereich von
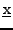 überabzählbar
unendlich ist, z.B. Reell.
überabzählbar
unendlich ist, z.B. Reell.
- Wahrscheinlichkeitsdichte
-
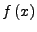
- ist nur für stetige Verteilung definiert
-
![$ f\left(x\right)dx=Pr\left[x<\underbar{x}\le x+dx\right]$](img24.png)
-
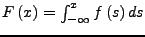
- Moment
- das
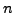 -te Moment einer Verteilunsfunktion
-te Moment einer Verteilunsfunktion
![$ E\left[\underbar{x}^{n}\right]=\int_{-\infty}^{\infty}s^{n}dF\left(s\right)$](img27.png)
- Erwartungswert
-
![$ E\left[x\right]==\int_{-\infty}^{\infty}sdF\left(s\right)$](img28.png)
- Entspricht erstem Moment
- auch Mittelwert genannt
Varianz
- Auch Streuungsquadrat
-
![$ E\left[\left(\underbar{x}-a\right)^{2}\right]=\sigma^{2}\left(\underbar{x}\right)+\left(E\left[\underbar{x}\right]-a\right)^{2}$](img30.png)
- Bedingte Wahrscheinlichkeit
-
![$ Pr\left[A\vert B\right]=\frac{Pr\left[A\wedge B\right]}{Pr\left[B\right]}$](img31.png)
- Wahrscheinlichkeit das
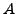 eintritt wenn mann bereits weiss, das
eintritt wenn mann bereits weiss, das
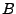 eintritt
eintritt
-
![$ Pr\left[A\wedge B\right]$](img34.png) Wahrscheinlichkeit das
Wahrscheinlichkeit das 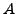 und
und 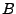 zusammen
eintreten
zusammen
eintreten
- Unabhängigkeit
- zweier Ereignisse
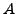 und
und
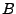 , wenn
, wenn
![$ Pr\left[A\vert B\right]=Pr\left[A\right]$](img35.png)
- negativ exponentielle Verteilung
-
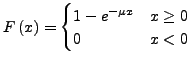
- Wahrscheinlichkeitsdichte
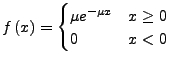
- Varianz
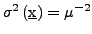
- Dies ist die einzige Verteilungsfunktion die Gedächnislos ist. D.h.
es gilt
- Wenn im Mittel zwischen zwei Aufträgen
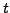 Zeiteinheiten vergehen,
dann muss man im Mittel trotzdem noch
Zeiteinheiten vergehen,
dann muss man im Mittel trotzdem noch 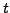 Zeiteinheiten warten, unabhängig
davon, wieviel Zeit schon vergangen ist.
Zeiteinheiten warten, unabhängig
davon, wieviel Zeit schon vergangen ist.
Warteschlange Allgemein
- Anschauung
- siehe Abbildung cap:WarteschlangeAnschaulich
Figure:
Warteschlangenmodell - Anschaulich
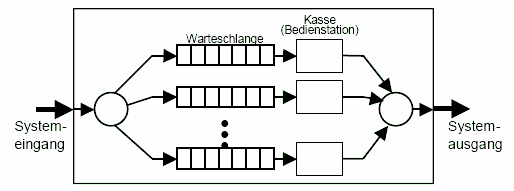 |
- Beschreibung
- siehe Abbildung cap:WarteschlangeAbstrakt
Figure:
Warteschlangenmodell - Abstrakt
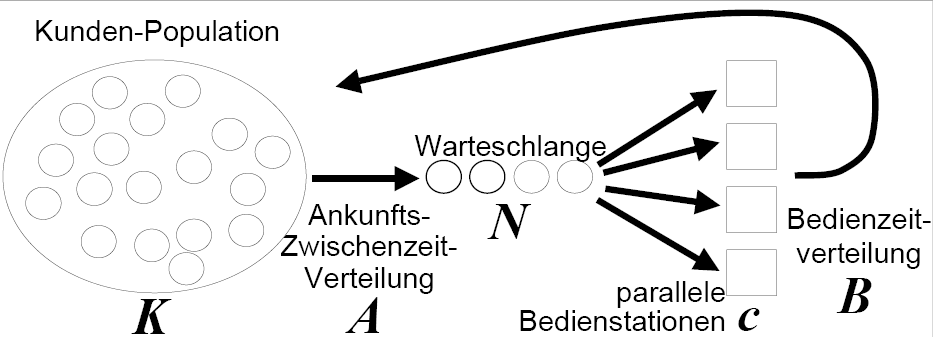 |
- Charakterisierung
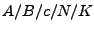
- Kundenpopulation
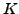
- Ankunftszwischenzeitverteilung
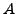
- Warteschlangenlänge
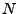
- Bedienstationenanzahl
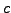
- Bedienzeitverteilung
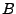
- Abkürzungen
- (typische)
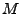 (negativ) exponentialverteilt
(negativ) exponentialverteilt
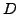 deterministisch oder konstant verteilt
deterministisch oder konstant verteilt
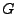 beliebig verteilt
beliebig verteilt
- z.B.
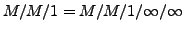
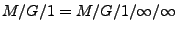
- Ankunftsrate
- (mittlere)
![$ \lambda=E\left[A\right]$](img50.png)
- Bedienrate
- (mittlere) pro Station
![$ \mu=E\left[B\right]$](img51.png)
- Streuung Bedienrate
-
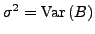
- Kunden im System
-
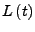 zum Zeitpunkt
zum Zeitpunkt 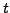
- Langzeitverhalten
-
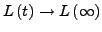 stationäre Verteilung
stationäre Verteilung
- Ziel der Warteschlangentheorie ist es diese Größe zu bestimmen
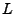 Erwartungswert von
Erwartungswert von
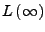
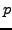 Langzeitausnutzung der Server
Langzeitausnutzung der Server
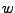 Langzeitaufenthaltzeit im System
Langzeitaufenthaltzeit im System
- Gesetz von Little
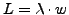
- Bedingung
- für die Stationarität
![$ E\left[A\right]=\lambda<\mu=E\left[B\right]$](img59.png)
- Langzeitausnutzung
- des Servers
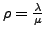
- Kunden im System
-
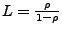
- Langzeitaufenthaltszeit
-
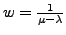
- Dichtefunktion
- von
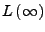
- dies ist die geometrische Verteilung
- Eigenschaften
-
- Warteschlangen werden länger, wenn bei konstanten Erwartungswert die
Streuung der Bedienzeiten wächst
- Jede Pufferlänge tritt mit gewisser Wahrscheinlichkeit einmal auf,
d.h. Puffer laufen stets gelegentlich voll
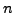 Server mit einer gemeinsamen Warteschlange sind besser als
Server mit einer gemeinsamen Warteschlange sind besser als 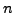 Server mit
Server mit 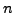 Warteschlangen
Warteschlangen





Next: Petrinetze
Up: Diskrete Modellierung und Simulation
Previous: DEVS
Contents
Index
Marco Möller 17:20:55 24.10.2005
![$\displaystyle \sigma^{2}=E\left[\left(\underbar{x}-E\left[\underbar{x}\right]\r...
...{-\infty}^{\infty}\left(s-E\left[\underbar{x}\right]\right)^{2}dF\left(s\right)$](img29.png)